Tabla de contenidos
¿Qué es una ecuación?
Desde desde las matemáticas una ecuación es una igualdad entre dos expresiones, cada una de las expresiones se conoce como miembro de la ecuación, están separadas por un signo igual (=) y la igualdad puede contener una o más incógnitas sin que sean resueltas.
Cuando se conocen los valores estos se pueden expresar a partir de números, coeficientes o constantes, cuando no se conocen los valores se conoce como incógnitas y se expresan normalmente con letras.
Partes de una ecuación
Una ecuación está compuesta por varias partes, estas partes se conocen como elementos de ecuación y son:
- Términos
- Términos independientes
- Igualdad
- Miembros
- Incógnitas
Se encuentran de la siguiente forma
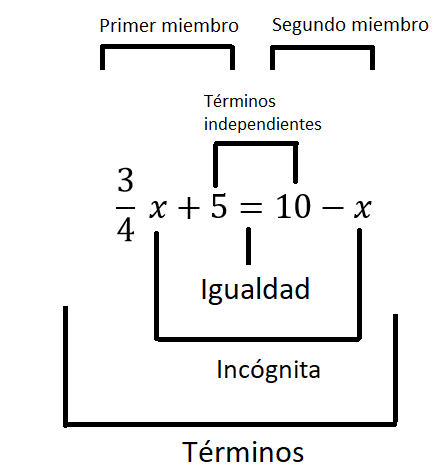
¿Todas las ecuaciones tienen solución?
No todas las ecuaciones tienen solución, para tenerla ambas partes a cada lado del igual deben cumplir con la condición de igualdad, por ejemplo:

Esta ecuación tiene como solución x=2 cuando eso pasa tanto la parte de la izquierda como la parte de la derecha cumplen con la condición de igualdad 7=7, sin embargo hay ecuaciones que sin importar el valor que se le asigne a x nunca se cumple la igualdad, por ejemplo:
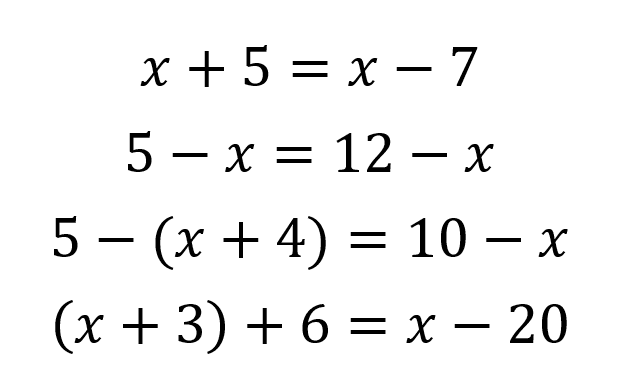
En ninguna de estas 4 ecuaciones existe un valor de x que permita obtener la condición de igualdad a ambos lados por lo que se puede asegurar que la ecuación sin solución.
¿Cómo resolver una ecuación?
El procedimiento para resolver una ecuación es sencillo solo depende si tiene paréntesis o denominadores, los pasos son:
- Resolver los paréntesis
- Quitar los denominadores
- Agrupar las variables x en un miembro y las variables independientes en otro
- Reducir términos semejantes
- Despejar la incógnita
Ejemplo de solución de una ecuación
Para poner en práctica el procedimiento para resolver una ecuación vamos a encontrar el valor de x en el siguiente ejercicio:

El primer paso es resolver los paréntesis, en este ejemplo solo hay uno, recuerda que para resolver ese tipo de paréntesis se debe multiplicar el número fuera del paréntesis por cada uno de los valores de adentro, en este caso la ecuación quedaría:

Al no haber paréntesis y tampoco haber denominadores el siguiente paso es agrupar las variables x en un miembro y las variables independientes en otro quedando:
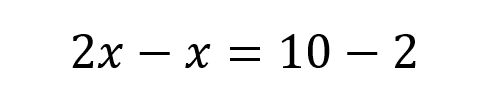
Recuerda que cuando los valores cambian de posición respecto al signo igual, ocurre también un cambio de signo así:
- Si está sumando pasa a restar
- Si está restando pasa a sumar
- Si está multiplicando pasa a dividir
- Si esta dividiendo pasa a multiplicar
Después el paso a seguir es reducir términos semejantes, por lo que nuestra ecuación quedaría:

De este modo se encuentra el valor de la incógnita.
¿Qué es el grado de una ecuación?
El grado de una ecuación es el mayor exponente al que se encuentran elevadas las incógnitas, por ejemplo:

Esta ecuación es de grado 3 debido a que el mayor exponente en las incógnitas es 3. Ahora veamos otro ejemplo:

En este segundo ejemplo el grado de la ecuación es 2, si bien el 6 está elevado a la 5 NO ES UNA INCÓGNITA por lo que no se tiene en cuenta a la hora de designar el grado de la ecuación.
Existen diferentes características y particularidades en el estudio de las ecuaciones de acuerdo con el grado, por esto te invitamos a conocer a mayor profundidad este tipo de ecuaciones haciendo click en los enlaces a continuación:
Ecuación de tercer grado
Ecuación de cuarto grado
Ecuación de quinto grado
¿Puede haber más de una incógnita en la ecuación?
Existen ocasiones en que las ecuaciones tienen más de una incógnita y es completamente normal, pueden haber 2, 3, 4 e incluso más incógnitas.
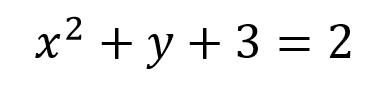
Por ejemplo en este caso se tienen dos incógnitas, es necesario resaltar que para poder solucionar los ejercicios que se le lleguen a plantear se necesitan tantas ecuaciones como incógnitas, es decir si hay dos incógnitas se necesitan dos ecuaciones para poder resolver el ejercicio, si se tienen 4 incógnitas, se necesitarán entonces 4 ecuaciones para poder encontrar la solución de cada una de ellas, a esto se le conoce como sistema de ecuaciones.
Tipos de ecuaciones
Existen diferentes tipos de ecuaciones, a continuación se van a nombrar las principales y para poder conocer más a fondo sobre cada una de ellas lo invitamos a que le de click a los enlaces, así pues, las ecuaciones se agrupan principalmente en:
- Ecuaciones algebraicas
- Ecuaciones trascendentes
- Ecuaciones funcionales
- Ecuaciones integrales
- Ecuaciones diferenciales
¿Para qué sirven las ecuaciones?
Las ecuaciones tienen un sin fin de aplicaciones en diferentes aspectos de la vida cotidiana y la vida profesional ya que permiten transformar problemas de igualdades a expresiones matemáticas para el desarrollo.
Ejemplo del uso de las ecuaciones en la vida cotidiana
Juan realiza la compra de unos zapatos y de una maleta, en total gasta 300 dólares, si solo los zapatos costaban 200 dólares ¿cuánto costó la maleta?
Solución
Aunque el ejercicio parece muy sencillo e inclusos se puede resolver mentalmente, la solución matemáticamente se expresa a partir de una ecuación así:
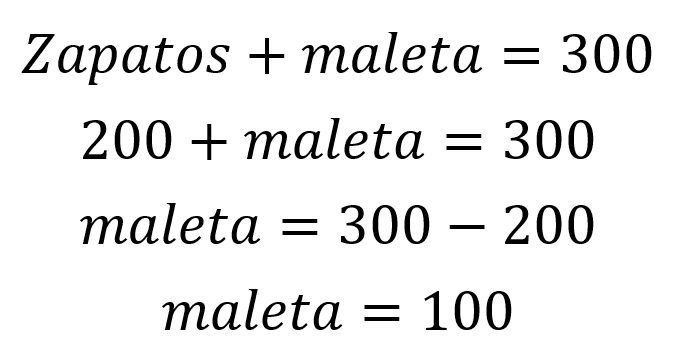
Ejemplo del uso de las ecuaciones en la vida profesional
Dentro de las diferentes profesiones existe un gran número de ecuaciones que permiten mostrar el comportamiento de diferentes fenómenos en los ámbitos de las ciencias naturales, la ingeniería, la medicina, entre muchas otras.
En nuestra página ecuacionde.com podrás descubrir el maravilloso mundo de las ecuaciones, en este caso te dejamos la lista de algunas de las ecuaciones más utilizadas en matemáticas:
Ecuación de la distancia entre dos puntos
También puedes aprender desde los temas básicos como lo son:
