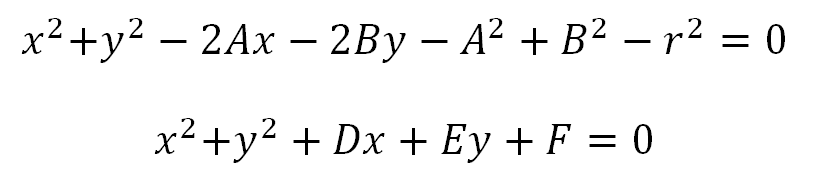Lo primero que debemos tener en cuenta es que la ecuación de la circunferencia describe el lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado centro.
La ecuación del círculo describe el lugar geométrico del conjunto de puntos cuya distancia al centro es igual o menor que el radio.
´De este modo la diferencia entre circunferencia y círculo básicamente es que la circunferencia es únicamente es la línea curva que contiene y bordea, mientras que el círculo es esa línea más todo lo que contiene dentro.
Tabla de contenidos
Ecuación ordinaria de la circunferencia con centro C
Para determinar la ecuación ordinaria de la circunferencia se toma como ejemplo una circunferencia cualquiera con centro en un valor C con coordenadas (A,B) y cuyo radio (r) llega hasta el punto (x,y) como se muestra a continuación.
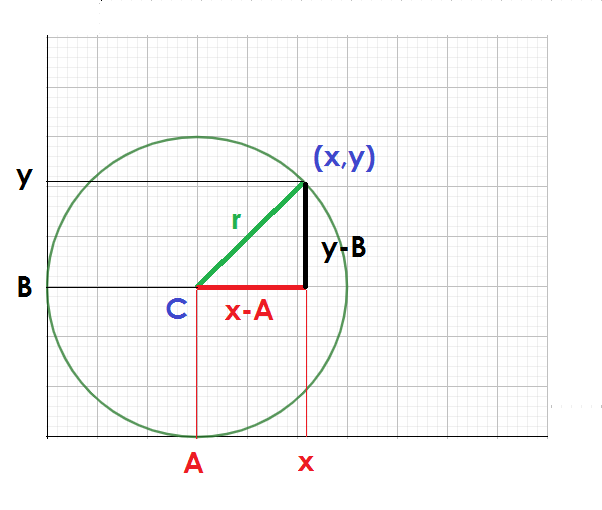
Teniendo en cuenta el triangulo rectángulo cuyos lados miden (x-A) y (y-B) y su hipotenusa es r y aplicando el teorema de Pitágoras se obtiene.
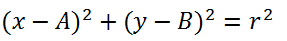
Nota: Si el valor de r es cero entonces no hay una circunferencia sino un punto.
Ejemplo resuelto ecuación ordinaria de la circunferencia con centro C
Calcular la ecuación de la circunferencia con centro en la coordenada (3,5) y de radio 3
Solución
Se utiliza la ecuación ordinaria de la circunferencia con centro C
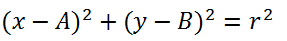
Se reemplazan los valores de la coordenada del centro (A,B) por los valores (3,5)
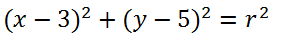
Luego se reemplaza el valor del radio
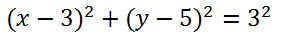
Finalmente resolviendo la ecuación se tiene
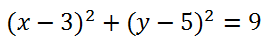
Ejercicios ecuación ordinaria de la circunferencia con centro C
Ejercicio ecuación de la circunferencia con centro en C
Ecuación canónica de la circunferencia
Cuando la circunferencia tiene el centro en el origen sin importar el radio se conoce como circunferencia canónica como la que se presenta a continuación.
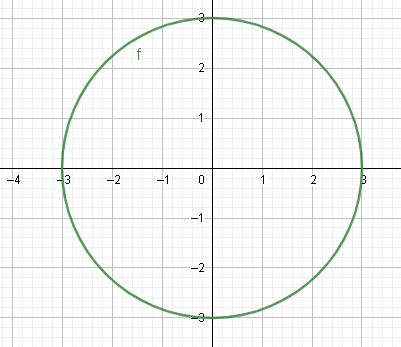
Esta circunferencia se puede describir con la ecuación canónica de la circunferencia.
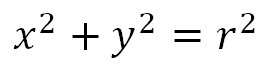
Por lo tanto la ecuación que representa la circunferencia de radio 3 con centro en el origen será:
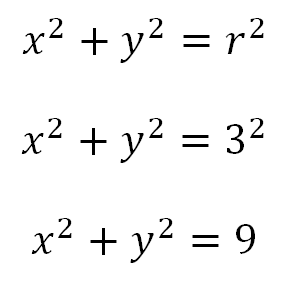
Ejemplo resuelto ecuación canónica de la circunferencia
Determinar la ecuación que describe a la circunferencia canónica y que pasa por el punto (3,4)
Solución
Se utiliza la ecuación canónica de la circunferencia
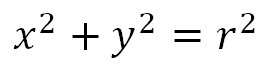
Se reemplazan los valores de (x,y) que se conocen, en este caso (3,4)
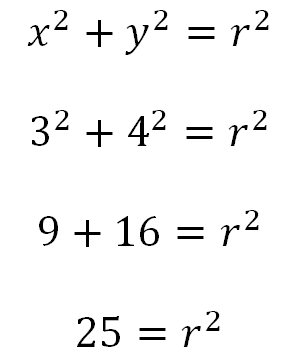
En este punto se puede conocer el radio de la circunferencia
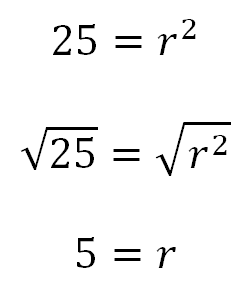
Finalmente se tiene toda la ecuación canónica para esta circunferencia
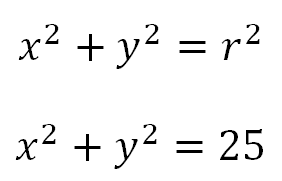
Ejercicios ecuación canónica de la circunferencia
Ejercicio ecuación canónica de la circunferencia
Ecuación general de la circunferencia
La última forma de escribir la ecuación de la circunferencia es mediante la ecuación general, simplemente es el desarrollo de la ecuación ordinaria con centro en C.
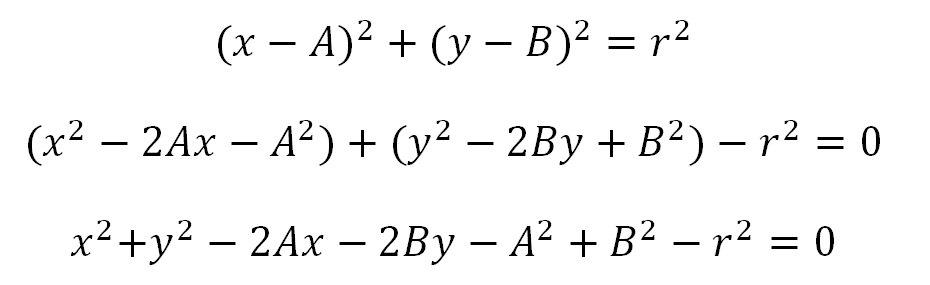
Luego se reemplazan los valores así:
-2A -> D
-2B -> E
-A^2+B^2-r^2 -> F
Se obtiene la ecuación general de la circunferencia