Primero vamos a empezar haciendo una definición de lo que es una recta y la diferencia que tiene con la ecuación de la recta.
Luego vamos a determinar la ecuación general y analizar las diferentes variantes que existen.
En la parte final vas a encontrar ejercicios resueltos paso a paso para que puedas comprender el tema a la perfección.
Tabla de contenidos
Definición de recta
Desde la geometría recta es una sucesión de puntos infinitos alineados en una misma dirección.
Cuando se mira en un plano esta recta puede ser vertical, horizontal o diagonal.
Definición de ecuación de la recta
Es la expresión algebraica que describe todos los puntos de la recta.
Al decir que describe se habla de la posición en el plano cartesiano tanto en el eje X como en el eje Y.
Ecuación general
La ecuación general de la recta describe el comportamiento de todas las rectas existentes en el plano cartesiano.
No importa la recta que se trace siempre va a cumplir con esta ecuación.
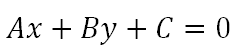
Esta ecuación general de la recta nace de uno de los teoremas de la geometría euclidiana que dice:
Para determinar una línea recta solo es necesario conocer dos puntos A y B.
La ecuación general de esa recta de primer grado es Ax + By + C = 0 , donde A, B, C pertenecen a los números reales; A y B son diferentes de cero simultáneamente.
Ecuación de la recta que pasa por un punto
Para determinar la expresión algebraica de la recta que pasa por un punto es necesario conocer la tanto la pendiente (m) como las coordenadas del punto (la abscisa X como la ordenada Y)
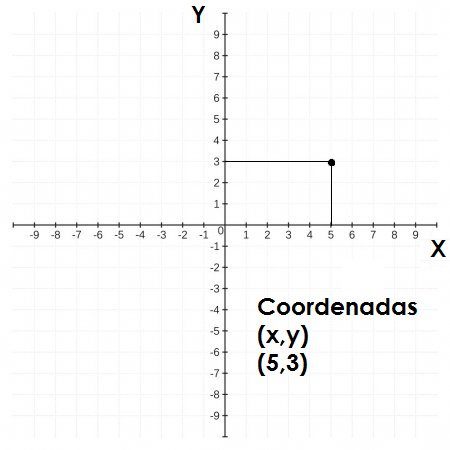
Antes de continuar debemos recordar que la ubicación del punto dentro del plano cartesiano se hace mediante el uso de coordenadas.
(x,y) es la manera en que se debe escribir la ubicación del punto, por ejemplo el siguiente punto se encuentra ubicado en la coordenada (5,3)
Ahora sí, la ecuación de la recta que pasa por un punto es la manera más sencilla de todos los casos de las expresiones algebraicas relacionadas con la recta.
La ecuación se escribe de la siguiente forma
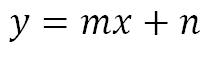
Ejemplo solucionado que pasa por un punto
Problema: ¿Cuál es la ecuación de la recta que pasa por el punto (1,5) y tiene una pendiente igual a 3?
Solución:
Se aplica la ecuación general para las ecuaciones de la recta que pasan por un punto:
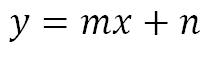
Conociendo la ecuación de la recta se reemplazan valores, recordemos que la pendiente es 3 y en este caso la coordenada del punto es (1,5) significa que x=1, y=5 por lo que la ecuación queda:
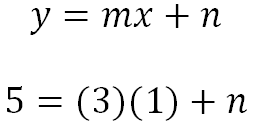
De esta ecuación se despeja n, quedando:
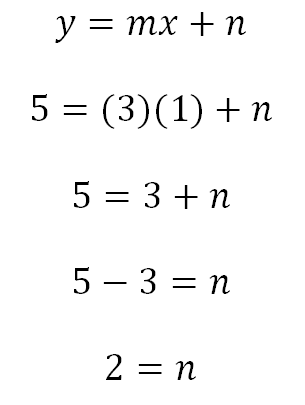
En conclusión la ecuación de la recta que pasa por el punto (1,5) y tiene una pendiente igual a 3 es:
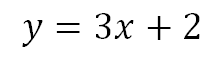
Ejercicios que pasa por un punto
Ejercicio #1 ecuación de la recta que pasa por un punto
Ecuación de la recta que pasa por dos puntos
Para determinar la ecuación de la recta que pasa por dos puntos es necesario conocer las coordenadas.
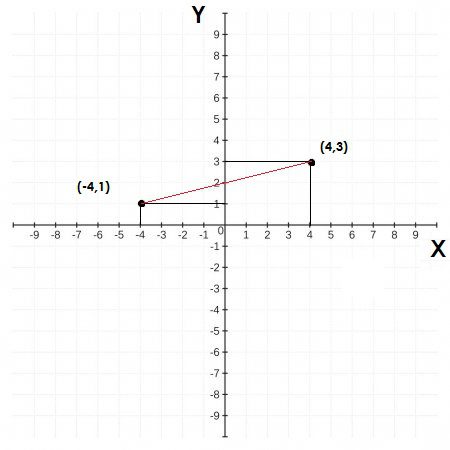
Tal como se muestra en el siguiente plano cartesiano
La ecuación que representa la recta que pasa por dos puntos es:
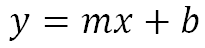
En esta ecuación m es la pendiente y b es el punto de corte con el eje y.
Ejemplo que pasa por dos puntos y corta el eje y
En este tipo de ejemplos la recta toca en alguno de los puntos el eje y, volvamos a la gráfica de los dos puntos anteriores

¿Cuál es la ecuación de la recta que pasa por los puntos (-4,1) y (4,3)?
La ecuación de esta recta será:
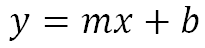
b es el punto de corte con el eje y, en este caso se puede evidenciar que la recta toca el eje y en el valor 2.
Por lo tanto nuestra ecuación queda:
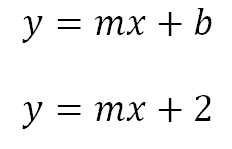
El siguiente paso es encontrar la pendiente (si no sabes cómo salió la ecuación de la pendiente y la diferente información que nos puede dar este valor númerico puedes aprenderlo todo haciendo click aquí)
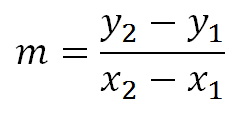
Se reemplazan los valores para encontrar la pendiente (recuerda que no importa el orden de los puntos)
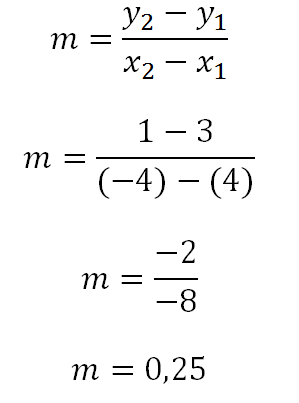
De este modo la línea recta que pasa por los puntos (-4,1) y (4,3) es
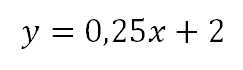
Ejercicio ecuación de la recta que pasa por dos puntos y corta el eje y
Ejercicio #2 Ecuación de la recta que pasa por dos puntos
Ejemplo que pasa por dos puntos y NO corta el eje y
En este tipo de ejemplos la recta no toca en ningún punto el eje y.
Por ejemplo, determine la ecuación de la línea que pasa por los puntos (5,3) y (9,7)
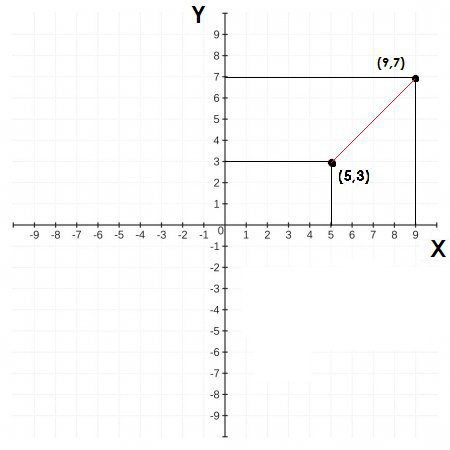
Solución:
En este tipo de ejercicios cuando no se corta el eje y lo primero que debemos hacer es calcular la pendiente mediante la ecuación:
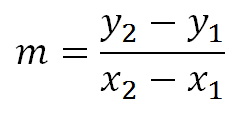
En este caso la pendiente será igual a:
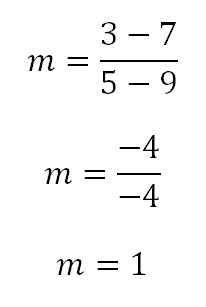
Teniendo en cuenta el resultado de la pendiente se reemplaza en la ecuación quedando:
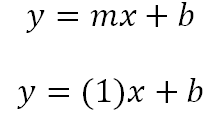
Ahora debemos calcular b (el punto de corte con el eje y) pero recordamos que gráficamente no se puede realizar como en el ejemplo anterior porque esta recta no corta el eje y.
Para solucionar esto debemos reemplazar los valores de x y de y por uno de los valores de la coordenada de un punto.
La recta pasa por los puntos (5,3) y (9,7) esto significa:
- Cuando x tiene un valor de 5, y tiene un valor de 3.
- Cuando x tiene un valor de 9, y tiene un valor de 7.
Para despejar b se puede utilizar cualquiera de los dos puntos, en este caso utilizaremos (5,3) pero si eres curioso intenta utilizar (9,7) verás que nos da el mismo resultado.
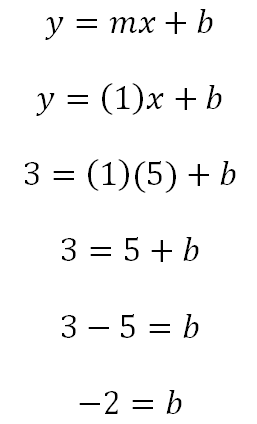
Ahora sí, podemos concluir que la ecuación de la línea que pasa por los puntos (5,3) y (9,7) es:
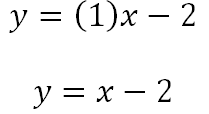
Como la pendiente era 1 y todo número multiplicado por 1 da el mismo número se puede omitir la escritura de ese valor.
Ejercicios que pasa por dos puntos y NO corta el eje y
Ejercicio #3 Ecuación de la recta que pasa por dos puntos y NO corta el el eje y
Ecuaciones de la recta perpendiculares una de otra
Para determinar la ecuación de una recta perpendicular a otra se debe conocer la ecuación de una de ellas.
Graficamente dos rectas son perpendiculares si se cruzan y forman un ángulo de 90° entre ellas.
Matemáticamente dos rectas son perpendiculares si al multiplicar las dos pendientes el resultado es -1.
Ejemplo:
Calcular la ecuación de la recta que es perpendicular a y=2x+1 y que pasa por el punto (2,0)
Solución:
Lo primero que se debe hacer es identificar el valor de la pendiente de la recta conocida.
La forma general de todas las ecuaciones de la línea recta es
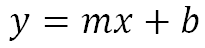
Entonces en la ecuación conocida se tiene que la pendiente es
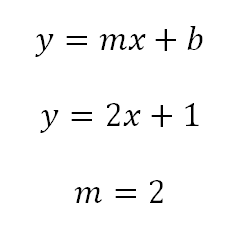
Encontrar el valor de la pendiente de la recta perpendicular, recordemos que al multiplicar las dos pendientes el resultado debe ser -1.
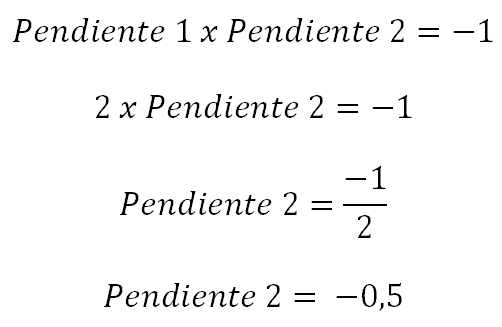
Conociendo que la recta perpendicular tiene como pendiente -0,5 ahora se reemplaza en la forma general.
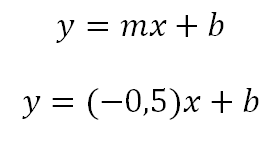
Para encontrar el valor de b en la ecuación reemplazamos los valores de x,y conocidos, es decir el punto por el que pasa la recta de acuerdo con el enunciado del problema (2,0) .
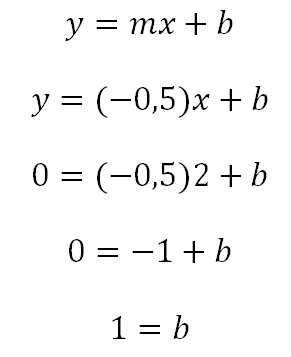
Ya se conocen todos los datos por lo tanto la ecuación que es perpendicular a y=2x+1 y que pasa por el punto (2,0) es
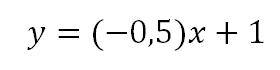
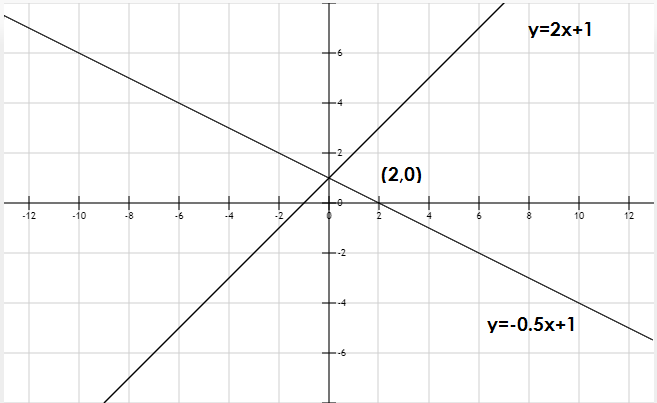
Finalmente para evidenciar que efectivamente una recta es perpendicular a la otra se grafican las dos ecuaciones y se ve que se forma un ángulo de 90° y que la recta pasa por el punto (2,0)
Ejercicio de rectas perpendiculares una de la otra
Ejercicio #4 Rectas perpendiculares una de la otra
Ecuaciones de la recta paralelas una de otra
Para determinar la ecuación de una recta paralela a otra se debe conocer la ecuación de una de ellas.
Gráficamente dos rectas son paralelas si nunca se tocan entre ellas.
Matemáticamente dos rectas son paralelas si las dos tienen las mismas pendientes.
Ejemplo
Calcular la ecuación de la recta que es paralela a y=2x+1 y que pasa por el punto (2,0)
Del ejemplo anterior habíamos demostrado que la pendiente de la ecuación conocida era 2.
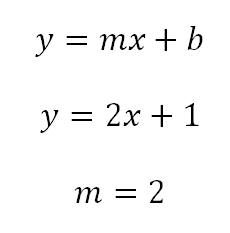
Entonces la ecuación de la recta paralela debe tener la misma pendiente es decir que la ecuación es
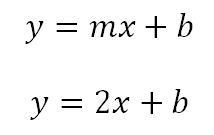
Como se sabe que pasa por el punto (2,0) se reemplazan los valores para despejar el valor de b.
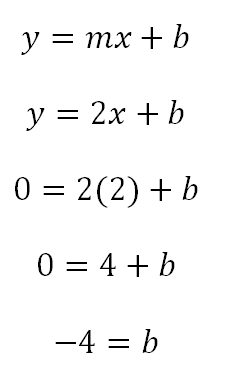
Conociendo los valores del punto de corte, b, y de la pendiente se reemplazan de tal modo que la ecuación que es paralela a y=2x+1 y que pasa por el punto (2,0) es
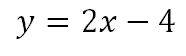
Finalmente para evidenciar que efectivamente una recta es paralela a la otra se grafican las dos ecuaciones y se ve que nunca se tocan y que la recta pasa por el punto (2,0)
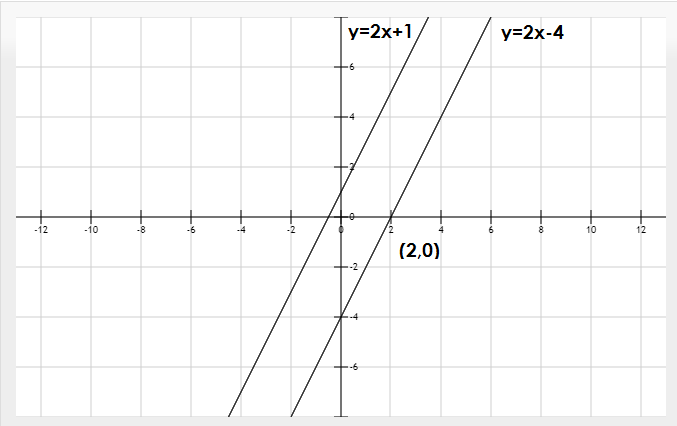
Ejercicio de rectas paralelas una de la otra
Ejercicio #5 Rectas paralelas una de la otra
Calculadora para hallar el punto de corte
En esta sección encontrarás la calculadora que te ayudará a hallar el punto de corte.
Para el uso de esta calculadora solo debes ingresar la pendiente y un punto de esta recta.
Calculadora para hallar la recta que pasa por dos puntos (x,y)
Ejercicios propuestos
1) ¿Cuál es la ecuación de la recta que pasa por el punto (0,3) y su pendiente es m=2?
¿Cómo referenciarnos?
Munévar, R. (S.F) Ecuación de la recta. ecuacionde.com. Recuperado el día (fecha en la que nos consultas) de https://ecuacionde.com/la-recta
Recuerda que si tienes dudas frente a este tema o cualquier otro tema relacionado con ecuaciones puedes dejar tu pregunta en los comentarios o en nuestra página de contacto

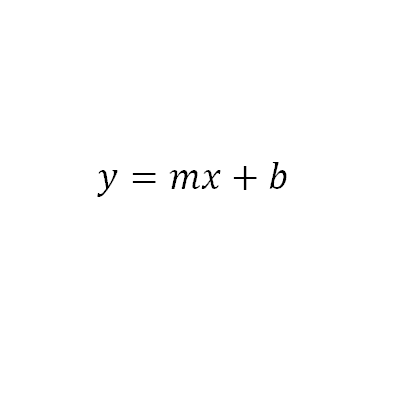
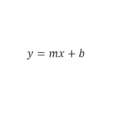
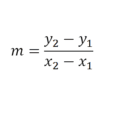
Hola profe. Me podria ayudar con ésta ecuacion de la recta. Se pide:
Hallar la ecuacion de la recta que tiene pendiente decreciente y corta al eje y en 4
Hola Richard, claro que sí, cuando te dicen que corta al eje y en 4 significa que cuando x tiene el valor de 0 y vale 4 es decir la coordenada es (0,4) hay infinitas rectas que pasan por ese punto y tienen la pendiente decreciente, te vamos a dejar tres ejemplos: y=-2X+4 y= -40X+4 o y=-100x+4 espero sea de ayuda
Excelente explicación, gracias Profesor.
Hola necesito ayuda cual es la formula general de la recta cuando es vertical y pasa por (-1,4), tengo entendido que para sacar la formula general de una recta necesito la pendiente y en este caso al ser vertical la pendiente es indefinida
Hola Kevin, efectivamente tienes razón, cuando una gráfica es representada por una línea vertical la pendiente es infinita, ahora necesitas que pase por el punto (-1,4). La dificultad del problema radica en que recta vertical debe cruzar por x=-1, si vemos el eje y no representa problema porque va a pasar por todos los puntos (-∞,∞). Ahora bien para «desplazar» la gráfica hasta el punto x=-1 solo debemos restarle al valor de x el punto que se necesita, para tu caso (x-(-1)) o sea (x+1). La recta vertical que cruza por el punto (-1,4) es y = ∞ (x+1) esperamos que tus dudas hayan sido resueltas, gracias por aprender con ecuacionde.com
necesitaria ayuda nnecesito graficar la funcion que tiene como pendiente m= indeterminada y un punto (0,5)
Hola Melina, gracias por dejar tus inquietudes, cuando la pendiente de una recta es indeterminada , dicha recta es vertical, en tu caso vertical a x=0 y que sube pasando por y=5 para que sea válida la coordenada (0,5)esperamos sigas disfrutando del maravilloso mundo de las ecuaciones
Me puedes ayudar con 8 ejercicios de ecuacion vectorial de la recta con su plana cartesiano por fa
Hola Cinthya, si quieres envíanos los ejercicios a [email protected] no te los vamos a resolver todos pero podemos subir una explicación que te permita resolverlos a ti
Sobre el ejercicio 4
¿Cuál de las siguientes rectas es perpendicular a y=-4x+6?
cuyo resultado es
y=(1/4)x+10
como se llega a 10?
Hola Mario, gracias por estudiar con Ecuacionde.com, la recta perpendicular a y=-4x+6 es aquella que al multiplicar su pendiente de como resultado -1, en este caso, y=(1/4)x+10 debido a que (1/4)x(-4)=-1. Sin embargo cualquier recta con pendiente (1/4x) va a ser perpendicular, el 10 es solo un ejemplo del valor pero por ejemplo las rectas y=(1/4)x+ 999, y=(1/4)x-432 también son perpendiculares. Esperamos haber sido de ayuda y recuerda seguir estudiando con nosotros.
Es una página muy eficiente y rapida, me ha servido mucho para comprobar si los ejercicios que hago están bien. Es una herramienta muy ultil para aprender si no tienes a quien preguntar acerca de ciertas situaciónes matemáticas
Excelente estábamos esperando una página aqui explican muy bien me ha servido muchísimo para las tareas gracias veo que encontramos de todos Los temas gracias