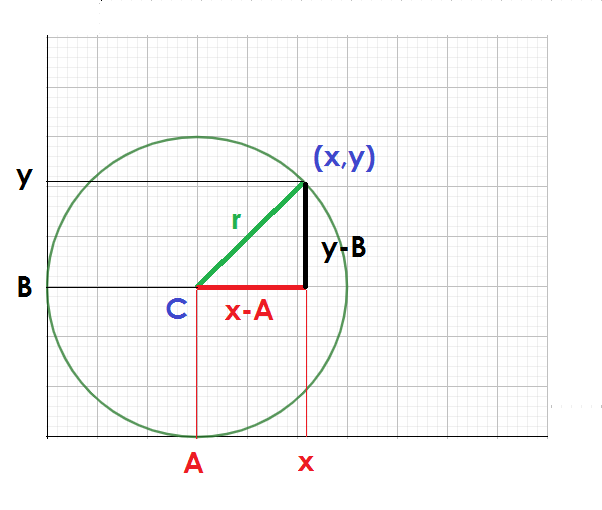
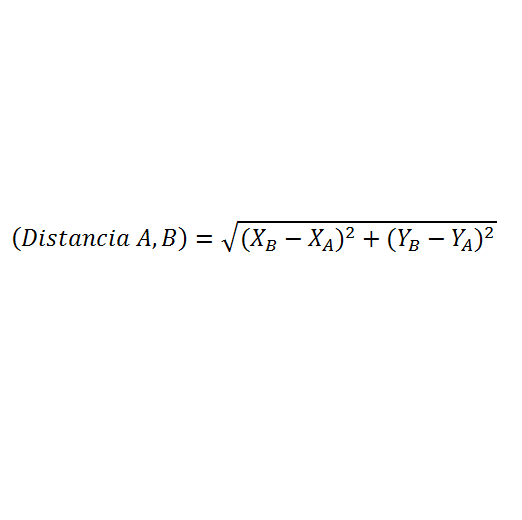La ecuación de la distancia entre dos puntos permite determinar la longitud del segmento que hay entre dos puntos dados.
Tabla de contenidos
Demostración de la ecuación de distancia entre dos puntos
Para definir la ecuación de la distancia entre dos puntos A y B primero se deben ubicar los puntos en el plano cartesiano.
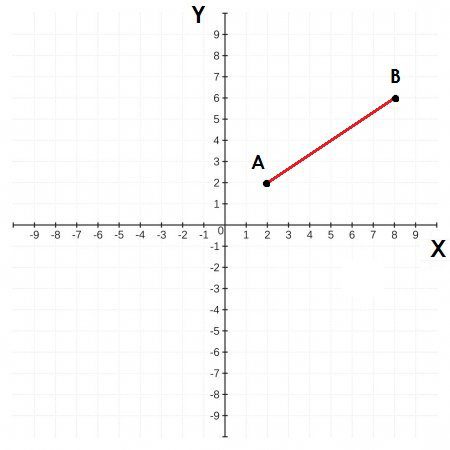
Luego debemos recordar que cada punto tiene su coordenada que se escribe de forma (x,y) de este modo quedaría
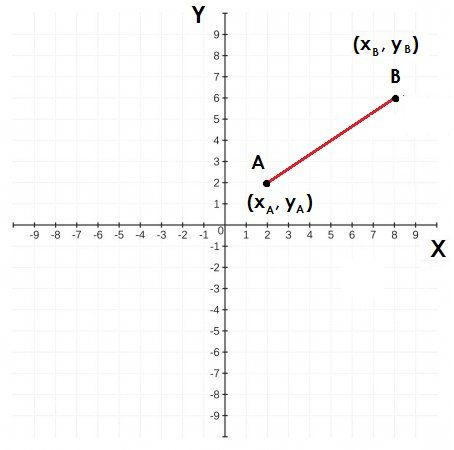
La distancia entre los puntos A y B se puede calcular a través del teorema de Pitágoras de la siguiente forma
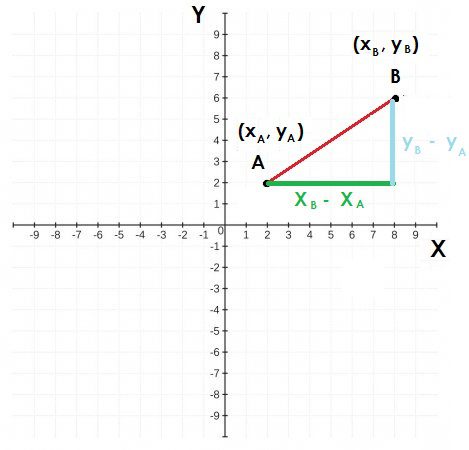
La hipotenusa es la distancia entre A y B y los lados del triangulo se obtienen a partir de las coordenadas x y y de cada punto.
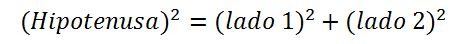
Reemplazando los valores del teorema de Pitágoras la ecuación de la distancia queda
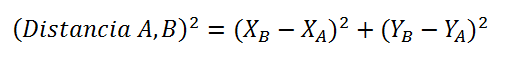
Despejando se tiene que la ecuación de la distancia entre dos puntos es:
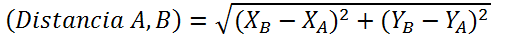
Ejemplos resuelto de la ecuación de distancia entre dos puntos
Ejemplo 1
Calcule la distancia que hay entre los puntos (1,5) y (3,15)
Solución
Se aplica la ecuación de la distancia entre dos puntos
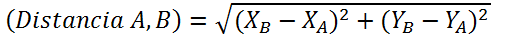
Se reemplazan los valores

La distancia entre los puntos (1,5) y (3,15) es 10,19803 que se aproxima a 10,20.
Ejemplo 2
Calcule la distancia que hay entre los puntos (-3,-8) y (4,11)
Solución
Se aplica la ecuación de la distancia entre dos puntos
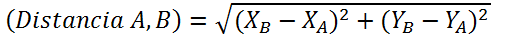
Se reemplazan los valores

Ejercicios ecuación de la distancia entre dos puntos
Ejercicio distancia entre dos puntos
Calculadora para la distancia entre dos puntos
En esta sección encontraras la calculadora que te ayudara a resolver la distancia entre dos puntos.
Para el uso de esta calculadora solo debes ingresar los puntos y dar clic en el botón de Respuesta. Divierte hallando la distancia entre dos puntos.