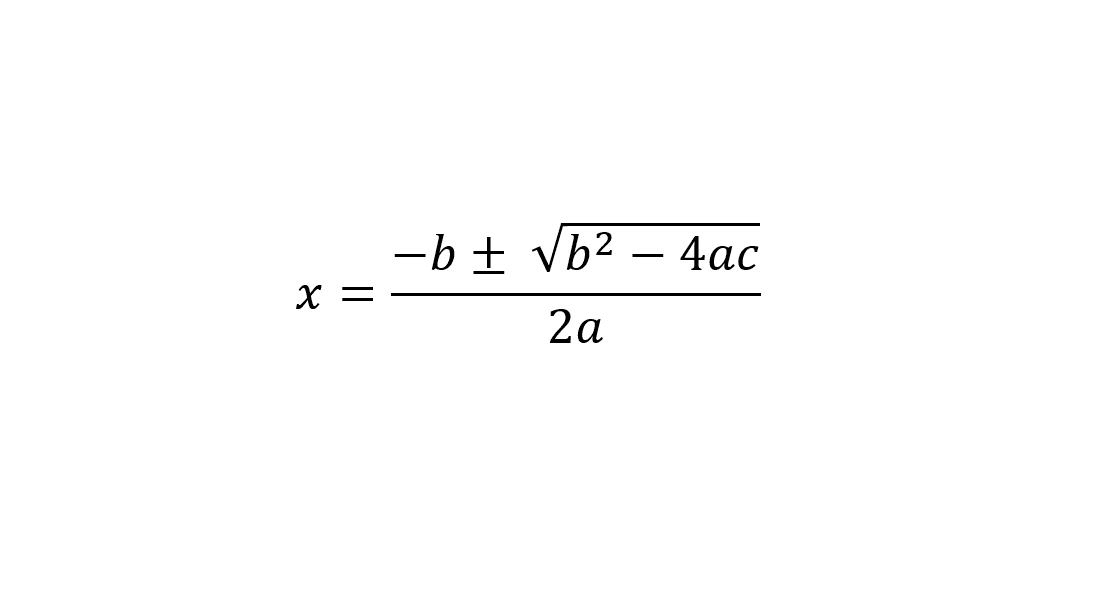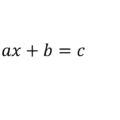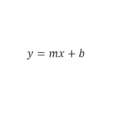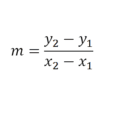Las ecuaciones de segundo grado también se conocen como ecuaciones cuadráticas por lo que cualquiera de las formas en las que se nombren se hace mención al mismo tipo de ecuación.
Tabla de contenidos
¿Qué es una ecuación de segundo grado?
En definición una ecuación de segundo grado o ecuación cuadrática es aquella que se puede escribir de la forma
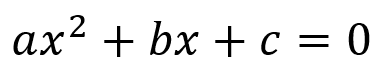
Siempre y cuando el valor de a sea diferente de cero.
En este caso x es la incógnita, a es conocida como coeficiente cuadrático, b es el coeficiente lineal y c es el término independiente, a, b y c son constantes.
Tipos de ecuación de segundo grado e identificación de constantes
No siempre las ecuaciones de segundo grado se encuentran escritas en su forma general por lo que es necesario aprender a identificar las diferentes formas de escritura.
Ecuación de segundo grado incompleto
Se considera una ecuación de segundo grado incompleta cuando el valor del coeficiente lineal o el valor del término independiente es igual a cero, es decir no se encuentra el valor de x sin potencia o no se encuentra una constante c.
Ejemplo 1
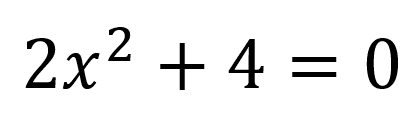
En este caso no se encuentra x sin exponente por lo que se puede deducir que el valor del coeficiente lineal b es igual a cero por lo que se consideraría una ecuación de segundo grado incompleta. En este caso las constantes serían:
a= 2
b= 0
c = 4
EJEMPLO 2
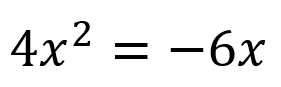
Este es un caso común en el que la ecuación no se encuentra igualada a cero y tampoco tiene una constante c que acompañe la expresión por lo que se consideraría una ecuación de segundo grado incompleta, si se reorganiza la ecuación a su forma original quedaría expresada como:
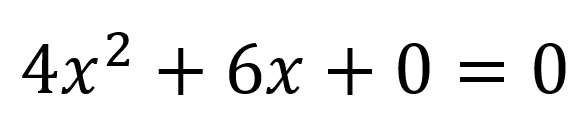
Teniendo como valor de los coeficientes:
a=4
b= 6
c=0
Ecuación de segundo grado completa
Este tipo de ecuación tiene todos los coeficientes diferentes de ceros y se puede escribir de la forma general.
Ejemplo 1
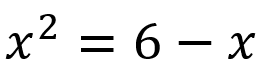
En este caso la ecuación no se encuentra igualada a cero tal y como se ve en la definición de ecuación de segundo grado, sin embargo cumple con todos los requisitos para serlo, haciendo un cambio en el orden de los factores esta ecuación se puede escribir de la forma:
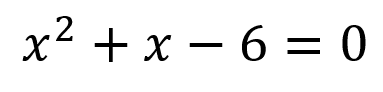
Recuerda que el cambio del signo se debe a que tanto el 6 como la x pasaron de un lado del igual al otro, de este modo se tiene que las constantes en esta ecuación son:
a = 1, como la x al cuadrado no tiene ningún número se deduce que el valor que lo acompaña es 1.
b=1, como la x no tiene ningún número se conoce que el valor que lo acompaña es 1.
c=-6, el valor de c puede tomar valores positivos o negativos.
¿Qué NO es una ecuación de segundo grado?
Identificar cuando una ecuación NO es de segundo grado es muy sencillo debido a que se conoce la forma general que deben tener estas.
Ejemplo 1
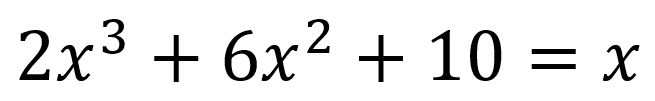
En este caso el mayor exponente de la ecuación es un 3, recordemos que una de las características que se deben cumplir para considerarse ecuación de segundo grado es que el mayor exponente debe ser 2.
Ejemplo 2
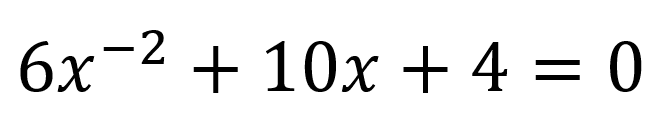
Para ser considerada una ecuación de segundo grado el valor del exponente 2 debe ser positivo, por lo que en este ejemplo al estar elevado a un exponente negativo no se puede considerar una ecuación de segundo grado.
Solución matemática de ecuaciones incompletas de segundo grado
Las soluciones de una ecuación cuadrática se definen como los valores que toma x para que la igualdad establecida se cumpla, normalmente al estar igualada en su forma general a cero las soluciones se conocen con el nombre de raíces, soluciones o ceros.
De acuerdo con el tipo de ecuación de segundo grado se puede establecer el procedimiento para la solución matemática, la solución gráfica se verá más adelante.
Solución de ecuaciones de segundo grado incompleta (sin coeficiente lineal «b»)
Cuando la ecuación de segundo grado no tiene el coeficiente lineal b queda expresada de la forma
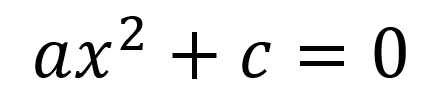
Despejando x se tiene que:
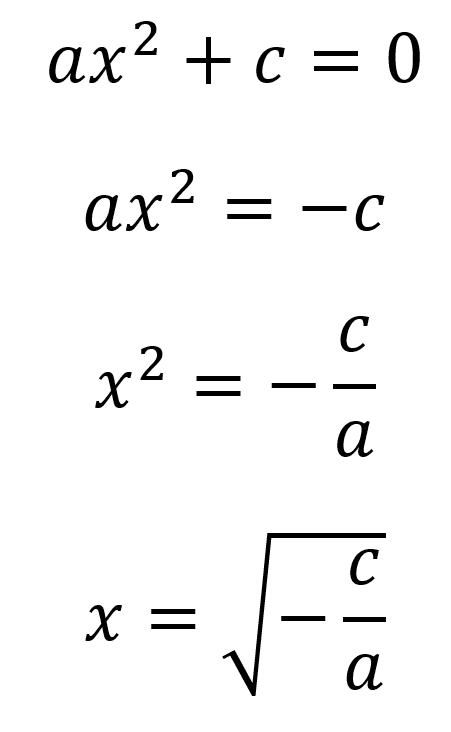
Las ecuaciones de segundo grado incompletas sin coeficiente lineal b tienen solución real siempre y cuando -c/a sea un número positivo, en caso de no ser positivo se tendrá solución en los números imaginarios.
Ejemplo 1
Se desea encontrar el valor de x que cumpla con la ecuación

Teniendo en cuenta el procedimiento anterior se despeja el valor de x:
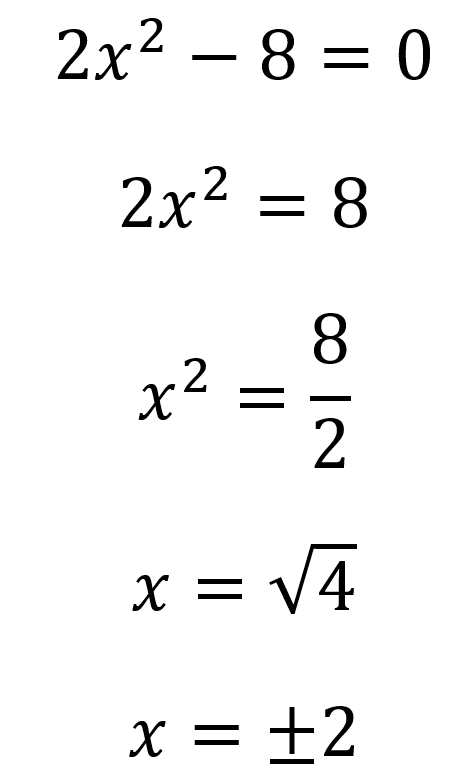
En este caso se puede evidenciar que la ecuación tiene dos soluciones diferentes, 2 y -2.
Solución de ecuaciones de segundo grado incompleta (sin término independiente «c»)
Cuando la ecuación de segundo grado no tiene el término independiente c queda expresada de la forma
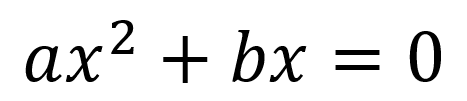
Despejando x se tiene que:
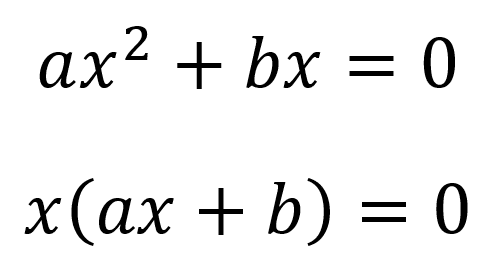
Para que la igualdad sea igual a cero existen dos posibilidades:
- x=0
- ax+b=0
En estos casos se tienen entonces dos soluciones:
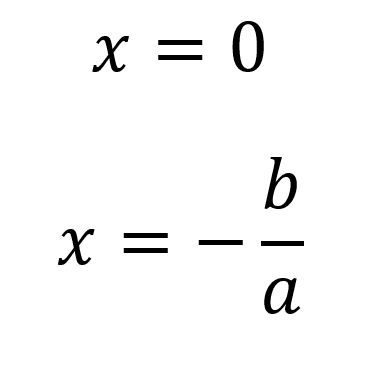
Ejemplo 1
Encontrar el valor de x en la ecuación
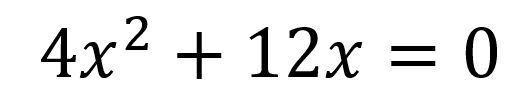
Teniendo en cuenta el procedimiento de factor común se tiene que las soluciones para esta ecuación son:
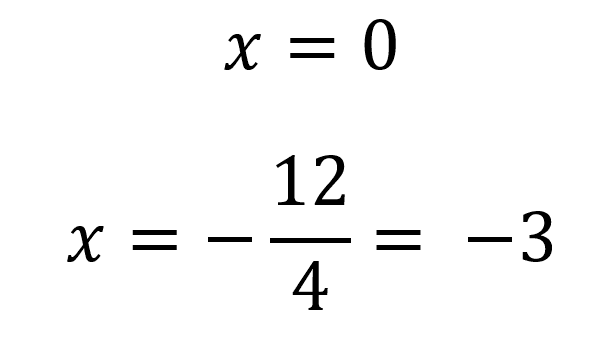
Esta ecuación tiene dos soluciones las cuales son x=0 y x=-3.
Solución matemática de ecuaciones completas de segundo grado
La forma más sencilla de solucionar ecuaciones completas de segundo grado es utilizando la fórmula cuadrática
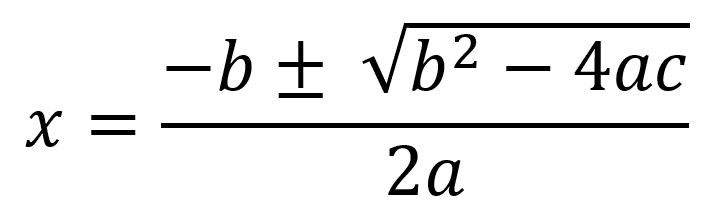
El número de raíces o soluciones dependen del discriminante (Δ) que se define como:
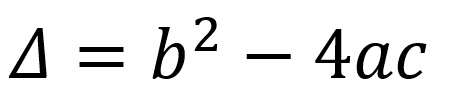
Luego, conociendo el discriminante se tienen tres diferentes opciones:
- Si Δ es mayor de cero: existen dos soluciones reales y distintas entre ellas.
- Si Δ es igual a cero: existe una única solución real.
- Si Δ es menor a cero: no tiene soluciones reales (puede tener solución en los números imaginarios)
Ejemplo solución de ecuación de segundo grado con determinante mayor de cero
Encontrar el valor de x que cumpla con la ecuación:
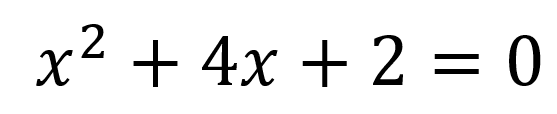
Lo primero que se debe realizar es identificar el valor de los coeficientes, en este caso:
a = 1
b= 4
c= 2
Una vez identificados se procede a calcular el determinante (Δ)
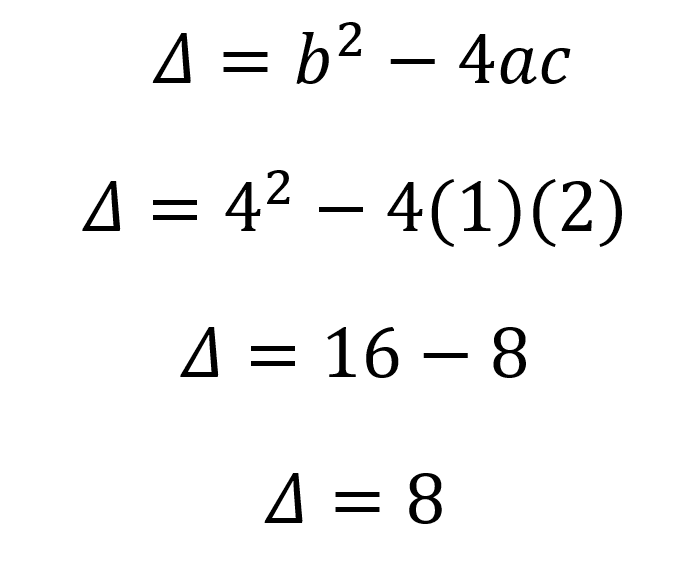
En este caso el determinante es mayor que cero por lo que de antemano se conoce que la ecuación cuadrática tendrá dos soluciones reales que se calculan a través de la fórmula cuadrática.
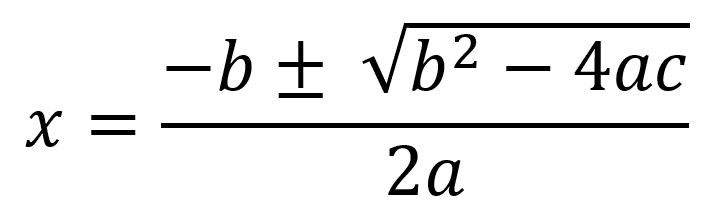
Debido a que existe el signo ± se deben hacer dos procedimientos por separado, el primero con el signo positivo, luego se procede con el signo negativo para calcular la segunda solución.
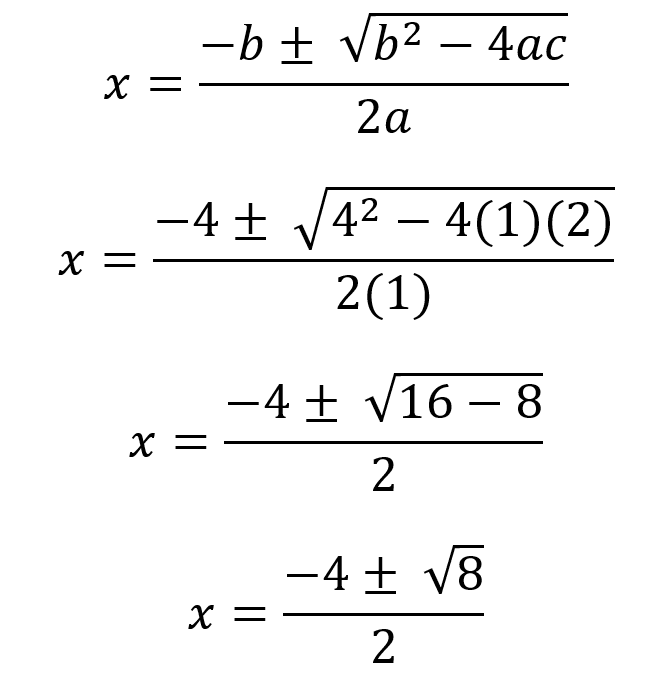
De este modo la primera solución es:
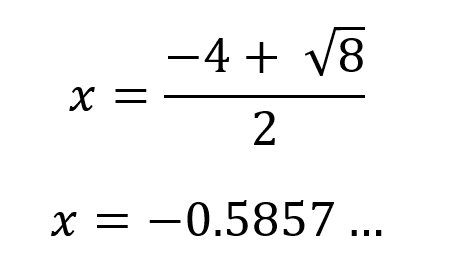
La segunda solución es:
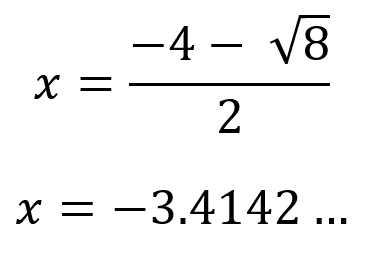
Solución de ecuaciones de segundo grado por factorización
En algunos casos la forma más sencilla es factorizar para encontrar los valores de x que permitan cumplir con la igualdad, teniendo en cuenta que la ecuación general de segundo grado se escribe de la forma
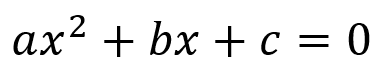
Se suponen dos valores que son solución para x, en este caso vamos a suponer que A y B son solución, de este modo la ecuación general se puede escribir como

Para encontrar los valores de una forma sencilla se debe cumplir que:
- A x B = c
- A+B = b
Veámoslo con un ejemplo, encontrar los valores de x que cumplen con la ecuación
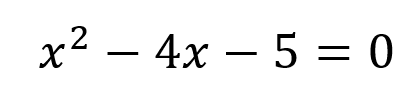
En este caso debemos encontrar dos números que al multiplicarse dan -5 y al sumarse dan -4.
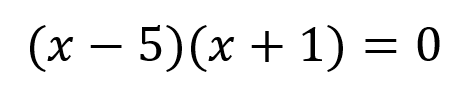
La solución que cumple con esas condiciones son -5 y 1 ya que:
- -5 x 1 = -5, que sería el valor de c.
- -5+1 = -4, que sería el valor de b.
Hay que tener en cuenta que solo hemos encontrado los números A y B, pero lo que nos preguntan son los valores de x para que se cumpla la igualdad, entonces cuando se están multiplicando dos números para que el resultado sea cero es porque uno de los dos tiene como valor cero, en este caso:
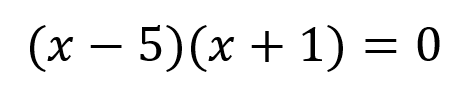
Se debe cumplir una de dos condiciones
- Que x-5 sea igual a cero
- Que x+1 sea igual a cero
Si x-5 es igual a cero significa que el valor de x debe ser 5
Si x+1 es igual a cero significa que el valor de x debe ser -1
De este modo se encuentran las dos soluciones de x que serían 5 y -1.
Solución de ecuaciones de segundo grado por gráfica
Es tal vez el método más sencillo para la solución de ecuaciones de segundo grado, simplemente se debe ver la gráfica de la ecuación y la solución será el valor de x cuando corta el eje, por ejemplo partiendo de la misma ecuación de segundo grado que factorizamos hace un instante.
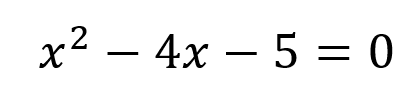
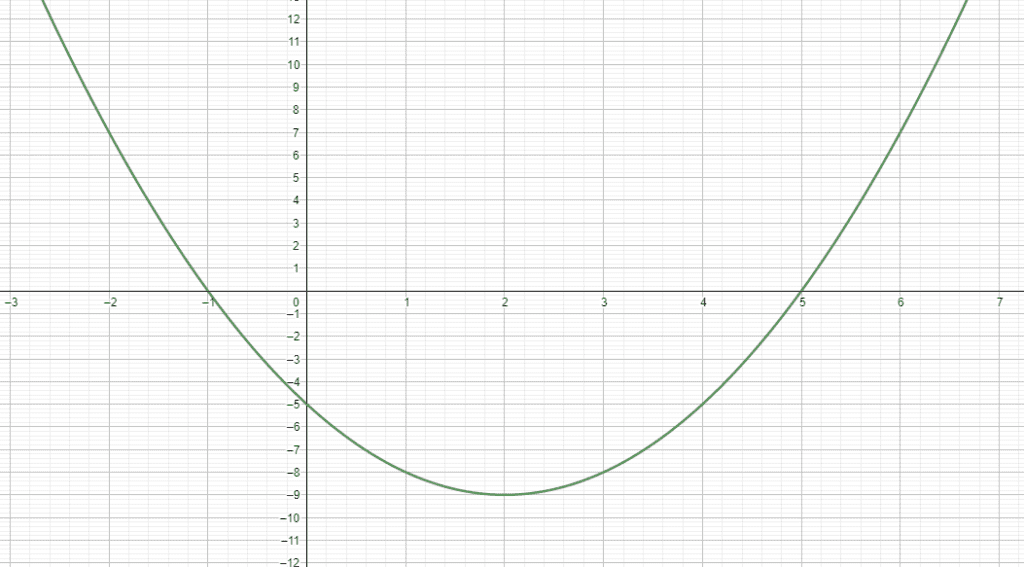
Se puede observar de una forma sencilla que la curva que representa la ecuación de segundo grado corta el eje x en los puntos x=5 y x=-1 por lo que se pueden encontrar las soluciones de forma rápida.