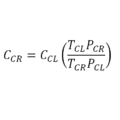La ecuación de Bernoulli es la forma de describir la ley de conservación de la energía de un fluido en movimiento.
A través de ella se puede expresar el comportamiento que tiene a lo largo de la tubería.

Tabla de contenidos
¿Qué establece el principio de Bernoulli?
Cuando un fluido está en movimiento a través de una tubería y se presentan cambios de diámetro, los segmentos donde el fluido se mueve más rápido se encuentra a menor presión que los segmentos donde el fluido se mueve más lento.
Parece ir en contra de lo que piensa la mayoría de las personas ya que muchos asumen que la velocidad alta depende de una alta presión en ese mismo punto.
La idea revolucionaría de Bernoulli fue demostrar que para que aumente la velocidad en un fluido se requiere que haya una presión más alta detrás del fluido que delante de él.
Condiciones para aplicar la ecuación de Bernoulli
La ecuación de Bernoulli describe el comportamiento de fluidos ideales los cuales cumplen con cuatro características fundamentales:
- Flujo constante: todas las partículas del fluido dentro de la tubería tienen la misma velocidad independientemente del punto en el que se encuentren.
- Flujo irrotacional: el fluido no posee velocidad angular neta, es decir, no existe posibilidad que se presenten remolinos dentro de la tubería.
- Flujo incompresible: esto significa que la densidad del fluido es constante en cualquier condición de presión.
- Flujo no viscoso: se considera que no existe (o al menos es insignificante) la fricción interna de las moléculas del fluido. Es decir, la capacidad de resistencia al movimiento tiende a cero.
Así mismo flujo debe ser isoentrópico, es decir:
- Los efectos externos sobre el flujo deben ser reversibles
- El sistema a estudiar debe ser adiabático, aparte de que el fluido no presenta flujo rotacional, la radiación de calor es nula o totalmente despreciable.
Demostración de la ecuación de Bernoulli
Para demostrar la ecuación de Bernoulli se puede tomar un ejemplo de la vida cotidiana como la que se muestra a continuación:
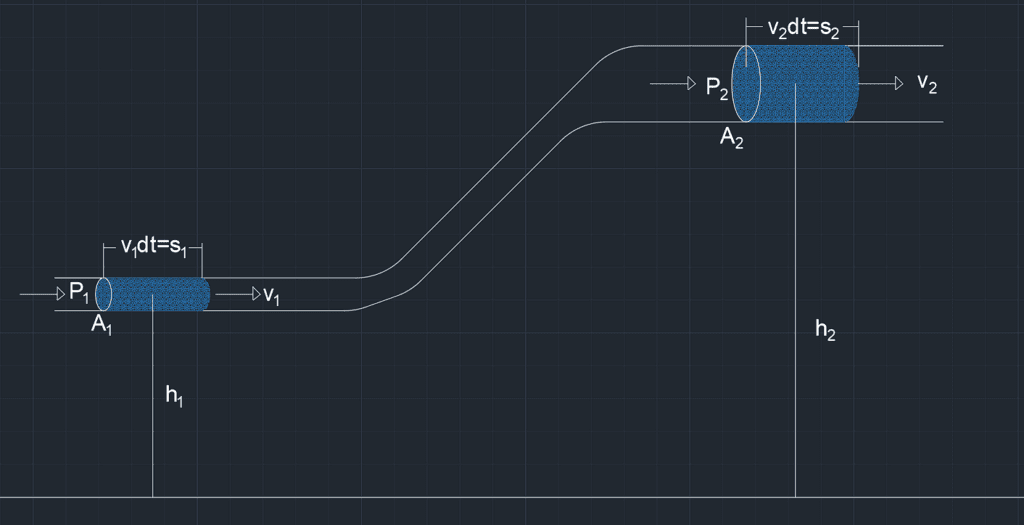
Se tiene una tubería circular con un área A1 a una altura h1 por la que fluye un fluido a una velocidad v1 con una presión P1 .
Avanza hasta una subida donde el fluido alcanza una altura h2 en ese punto el área se incrementa hasta A2 por lo que la velocidad también se modifica a v2 y la presión pasa a ser P2.
Cuando se aplica la segunda ley de Newton que relaciona la conservación del momento lineal al fluido a través de la tubería se conoce que:
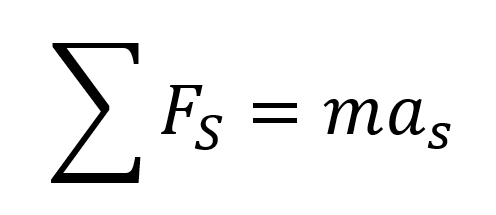
Como el fluido es ideal las fuerzas de fricción son despreciables, por lo que las fuerzas que interactúan sobre una partícula cualquiera son:

Como la partícula de fluido puede ir en cualquier punto de la tubería es importante considerar el ángulo θ.
Esto es importante ya que en el momento de estudio puede estar subiendo con un grado de inclinación entre la línea de corriente y el eje vertical z.
Solución de la demostración
Debemos recordar que la masa es la densidad por el volumen y el volumen a su vez es relativo al área de la tubería y la distancia de segmento s que se esté estudiando por eso:
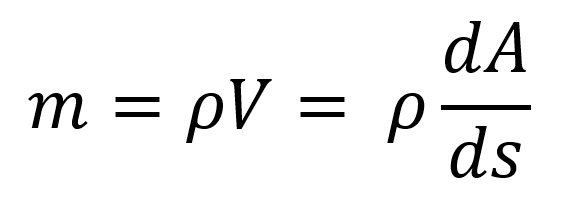
El peso del fluido es la masa por la gravedad, pero como dejamos expresada la masa en función de la densidad, el área y el segmento deducimos que:
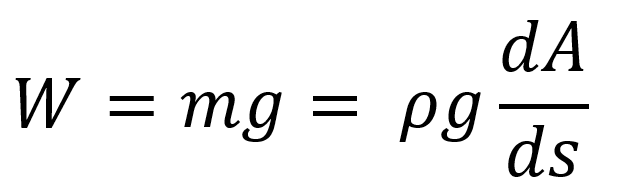
El seno del ángulo representa el cateto opuesto sobre el cateto adyacente que en el caso de la tubería serían la altura en el eje z y la longitud del segmento s respectivamente.
Por lo que:
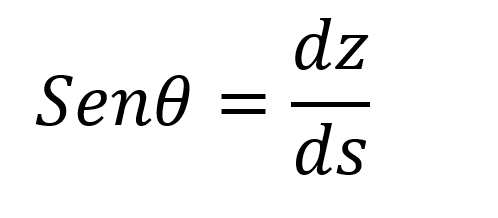
Sustituyendo los valores de peso y seno del ángulo en la ecuación del análisis de las fuerzas que interactúan en la partícula de fluido.
Se tiene que:

Sacando factor común dA en ambos lados de la igualdad y simplificando ds.
El proceso se hace en los términos donde se encuentra tanto en el numerador como en el denominador se obtiene la expresión derivada de la ecuación de Bernoulli:

Se integra la expresión en función de V recordando que:
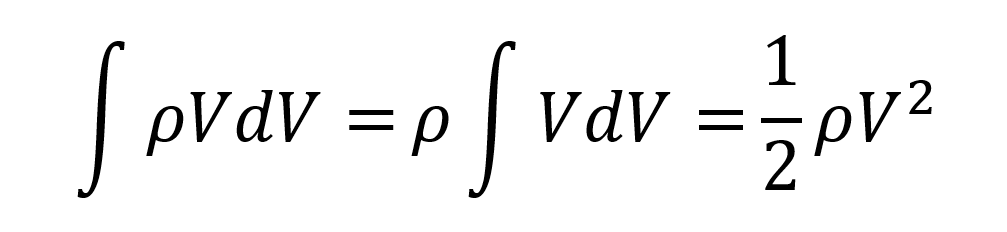
Se reordenan y reemplazan los valores para obtener:
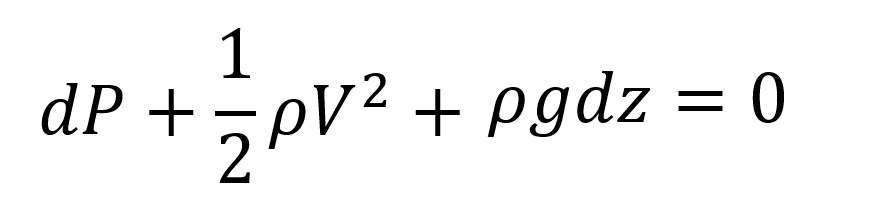
Ahora se dividen todos los términos entre la densidad para quedar:
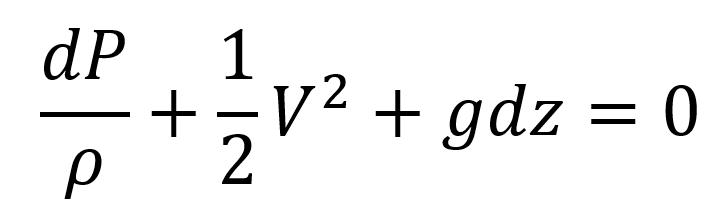
Se integra en función de la presión, recordando que se había asumido que el fluido era un líquido ideal, es decir que no presenta propiedades de compresión por lo que el volumen no depende de la presión.
La altura a la cual se encuentre el fluido tampoco depende de la presión por lo que se da la primera ecuación de Bernoulli llamada ecuación de flujo estacionario incompresible:
Ecuación de Bernoulli en flujo estacionario e incompresible
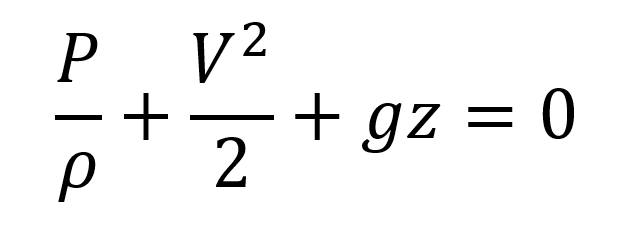
Esta ecuación es ampliamente utilizada en mecánica de fluidos para el flujo estacionario e incompresible a lo largo de una tubería.
La ecuación de Bernoulli también puede escribirse entre dos puntos, de hecho esta es la forma más conocida de hacerlo y la que se utiliza en la mayor parte de los ejercicios en la mecánica de fluidos.

¿Qué variables tiene en cuenta la ecuación de Bernoulli?
Al tener en cuenta la presión, velocidad y posición del fluido la ecuación de Bernoulli puede considerarse como una expresión del balance de energía mecánica.
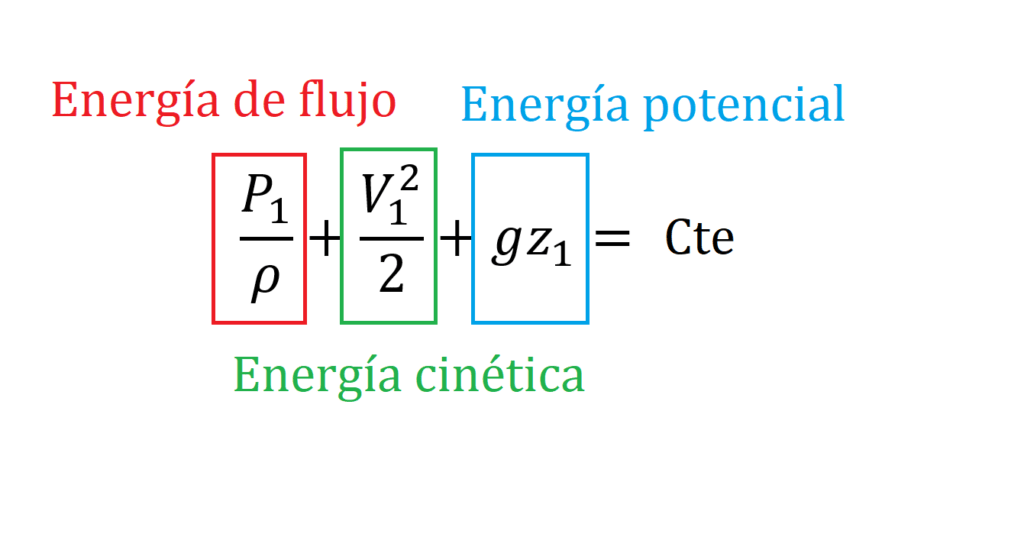
La ecuación de Bernoulli expresa que, en el transcurso del flujo estacionario e incompresible, con fricción despreciable, las diversas forman de la energía mecánica se transforman entre sí pero su suma permanece constante.
De este modo se puede conocer:
- Presión: la fuerza sobre área que se aplica al fluido en cualquiera de los puntos del sistema que se está estudiando
- Densidad: relación de masa sobre volumen del fluido, si no hay cambios en temperatura se espera a que esta propiedad se mantenga constante a lo largo de la tubería.
- Velocidad: distancia que recorre el fluido en un periodo de tiempo determinado.
- Altura: posición relativa respecto al eje z del fluido.
Aplicaciones del principio de Bernoulli
Algunas de las aplicaciones más interesantes de la ecuación de Bernoulli son:
Curva en una pelota de Béisbol
Cuando una pelota de béisbol no gira y se mueve por una corriente de aire mostrará un flujo simétrico, pero cuando se hace con giro se va a curvar el recorrido ya que el lado de la pelota que gira aumenta la velocidad del aire que fluye a través de ella y por principio de Bernoulli la presión del aire se reducirá.

Aunque es un fenómeno que se presenta por el principio de Bernoulli a través de las ecuaciones no se puede predecir con total exactitud la curvatura de la pelota, ya que además de todos los factores externos que pueden influir el aire es compresible y pueden haber cambios de presión.
Ala de un avión
El aire pasa a través de la parte superior del ala y al estrecharse las líneas de flujo se aumenta la velocidad relativa del aire en el ala, debido al principio de Bernoulli se produce una disminución de la presión en la parte superior y el avión puede elevarse.

Ejercicios resueltos de la ecuación de Bernoulli
La ecuación de Bernoulli tiene una gran utilidad en una gran variedad de fenómenos físicos por ejemplo:
Lanzamiento de agua al aire
Una mujer coloca su dedo pulgar para cubrir la mayor parte de la salida de una manguera cuya agua sale con una presión de 120 kPa.
Hace que el chorro salga hacía arriba con una velocidad de 0,1 m/s
¿Hasta qué altura llega el agua si se encuentra en un lugar donde la presión atmosférica es de 100 kPa?
Solución:
Lo primero que se debe hacer es plantear la ecuación de Bernoulli:

Reemplazamos los valores conocidos:

Recordemos que la densidad del agua es de 1000 kg/m3 y la gravedad es de 9,81 m/s2 de allí salen esos datos.
La altura inicial se asume como cero por lo que a partir de ese punto sale el agua.
La velocidad final también es cero porque se conoce que en el punto máximo de altura el agua se detiene para empezar a caer tal como se ve en los lanzamientos verticales.
Por lo que la ecuación queda reducida a:

Luego pasamos los kilo pascales a pascales y lo dejamos en sus respectivas unidades del sistema internacional de unidades.

Y se procede a despejar la altura z2
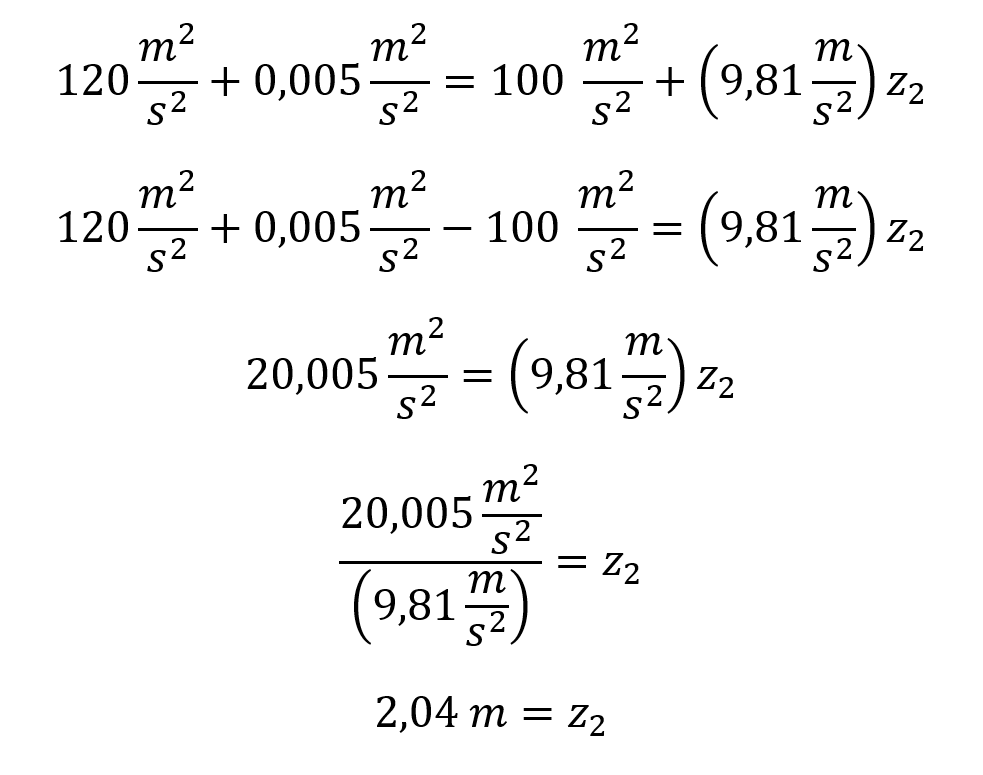
Descarga de agua desde un tanque grande
Un tanque grande que tiene 10 metros de altura está abierto a la atmosfera y totalmente lleno de agua.
En la parte inferior tiene una salida por una tubería pequeña, ¿a qué velocidad sale el agua?

Solución
Se debe plantear la ecuación de Bernoulli entre los dos puntos:

Como el tanque se encuentra abierto a la atmósfera y el agua sale en la parte inferior a la misma atmósfera se puede decir que P1 y P2 son iguales.
Adicional a esto la velocidad con la que baja el nivel del tanque es muy muy pequeña comparada con la velocidad con la que sale el fluido por el tubo por lo que V1 tiende a cero.
De este modo la ecuación se puede escribir:
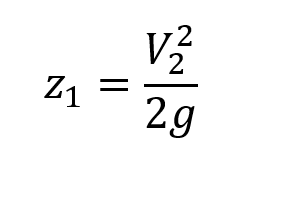
Despejando se tiene que:

Medición de la velocidad por medio de un tubo de Pitot
Un piezómetro y un tubo de Pitot están fijos a una tubería horizontal de agua con el fin de medir las presiones estáticas y de estancamiento (estática + dinámica)
¿Cuál es la velocidad de acuerdo con la ilustración que se presenta a continuación?

Solución
La presión estática en los puntos 1 y 2 son:
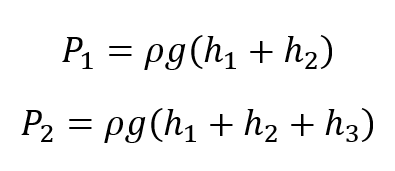
Posterior a esto se plantea la ecuación de Bernoulli:

Como el punto dos es un punto de estancamiento la velocidad final es cero, y la altura del punto 1 y del punto 2 son la misma.
Entonces se tiene que:
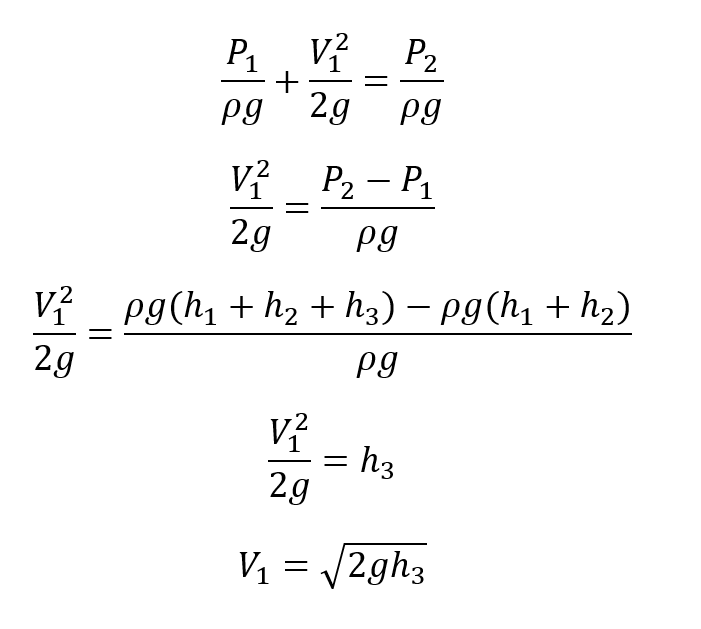
Reemplazando los valores se tiene que:
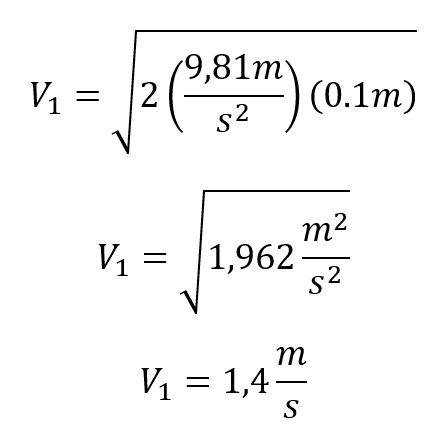
Limitaciones en el uso de la ecuación de Bernoulli
A pesar de que la ecuación de Bernoulli es bastante versátil y se utiliza en una gran cantidad de aplicaciones dentro de la mecánica de fluidos.
Sin embargo tiene una serie de limitaciones que son importantes conocer, estas son:
Flujo no estacionario
La ecuación de Bernoulli se utiliza únicamente en flujo estacionario.
No debe utilizarse cuando se tienen arranques o paradas espontaneas del fluido, ni se debe utilizar cuando el flujo es muy turbulento.
Flujo con fricción
Normalmente se hacen estudios de pequeños segmentos en tuberías por lo que se puede despreciar la fricción en la ecuación de Bernoulli.
Sin embargo cuando se tienen largos trazos la fricción empieza a jugar un papel importante por lo que es posible que no se cumpla la ecuación.
También cuando una línea de tubería tiene muchos accesorios que perturban la línea de la estructura de la corriente del flujo (por ejemplo codos, T, Y).
Cuando tiene muchos accesorios (manómetros, válvulas y otros) es posible que la fricción sea tanta que no se cumpla la ecuación de Bernoulli.
Trabajo en la línea de tubería
La ecuación de Bernoulli se dedujo haciendo el balance de fuerzas sobre una partícula del fluido.
No se puede aplicar si se le aplica trabajo a partir de una fuente externa como una bomba, una turbina, un ventilador o cualquier máquina del tipo impulsor.
Flujo compresible
Dentro de las suposiciones iniciales se tenía que el fluido no cambiaba de volumen por los efectos de la presión.
Sin embargo algunos fluidos no cumplen con esa condición por lo que es posible que la ecuación de Bernoulli no se cumpla.
¿Cómo referenciarnos?
Si deseas incluir esta información en alguno de tus trabajos no olvides referenciarnos, puedes hacerlo así:
Munévar, R. (10 de junio de 2022) Ecuación de Bernoulli. Ecuacionde.com. Recuperado el día/mes/año (inserta aquí la fecha del día que consultas nuestra web) de https://ecuacionde.com/bernoulli