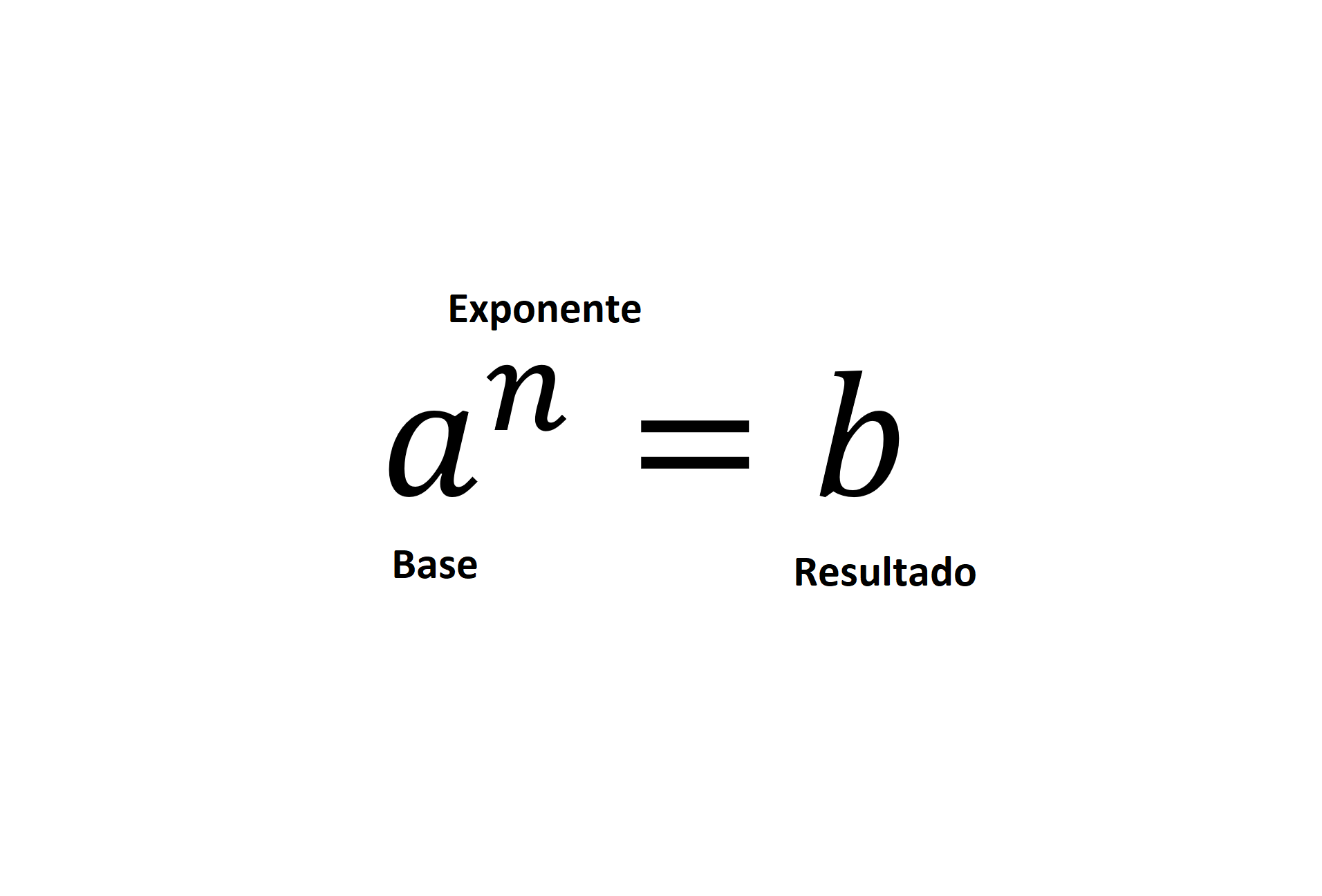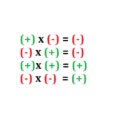En matemáticas, la potenciación o exponenciación es una operación que indica cuántas veces se multiplica un número por sí mismo, se utiliza en diferentes ramas del conocimiento general desde la aritmética básica hasta la ingeniería.
Por ejemplo,
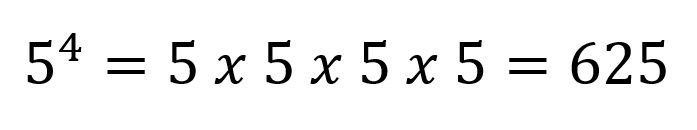
Tabla de contenidos
Partes de la potenciación
Existen tres partes fundamentales cada vez que llevamos a cabo este proceso, la base, el exponente y el resultado.
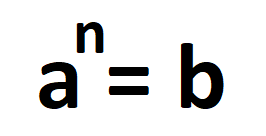
Base
Representada por la letra a, es el número que se va a multiplicar.
Exponente
Es el número de veces que se va a multiplicar la base, se representa con la letra n.
Resultado
Es el valor número que da al multiplicarse la base el número de veces que indica el exponente.
¿Cómo se lee la potenciación?
Dependiendo del valor del exponente será la lectura de la potencia, para ello tenemos tres casos:
Cuando el exponente es 2
En este caso se lee la base y luego «al cuadrado» por ejemplo:
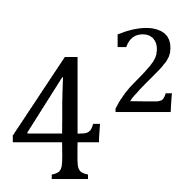
Esta expresión se leería «cuatro al cuadrado».
Cuando el exponente es 3
En este caso se lee la base y luego «al cubo» por ejemplo:

Esta expresión se leería «siete al cubo».
Cuando el exponente es diferente a 2 o a 3
Cualquier otro número diferente al 2 o al 3 cambia le forma en la que leemos la potencia, para este caso se lee la base y luego «elevado a la» y el número de del exponente, por ejemplo:
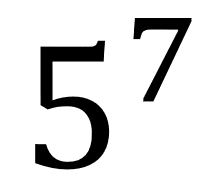
Esta expresión se lee «cinco elevado a la siete».
Calculadora de potenciación
Propiedades de la potenciación
Cuando se presentan operaciones matemáticas con potencias se pueden utilizar diferentes propiedades que tienen para facilitar el cálculo.
Las propiedades son variadas y dependen de la operación, estas son:
Exponente igual a cero
Todo número elevado a un exponente cero da como resultado uno, ejemplo:
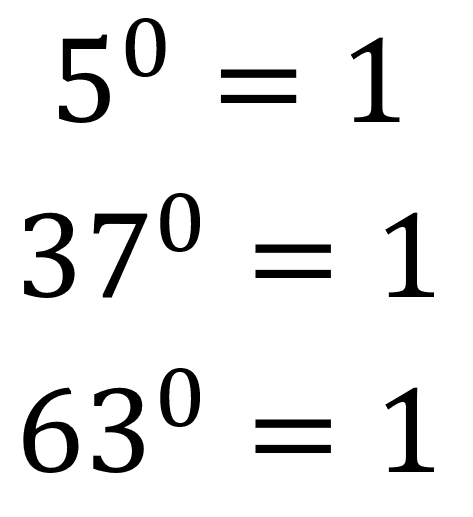
La forma general en que se escribe esta propiedad es:
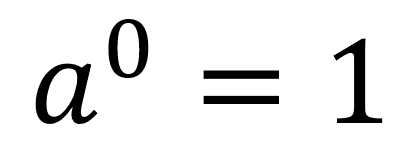
Exponente igual a uno
Todo número elevado a la uno, da como resultado el mismo número, ejemplo:
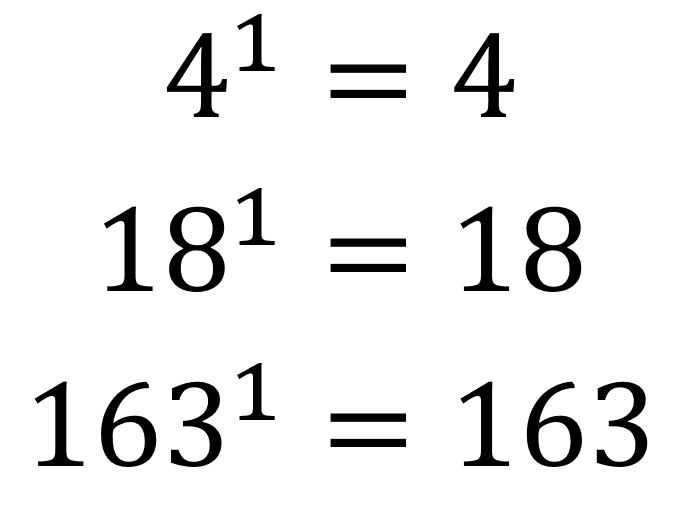
En general esta propiedad se expresa como:
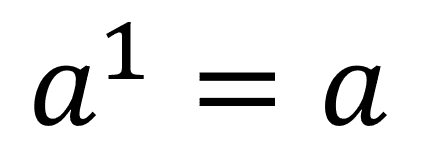
Producto de potencias con la misma base
Cuando se tienen dos potencias con la misma base y se quieren multiplicar, lo que se hace es dejar la misma base y sumar los exponentes, por ejemplo:
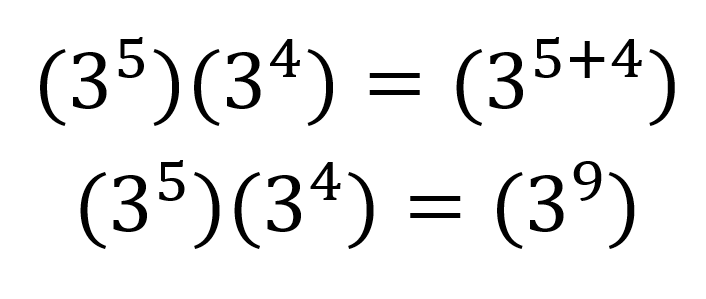
Esta propiedad solo se cumple si las dos bases son iguales.
La forma general de escribir esto es:
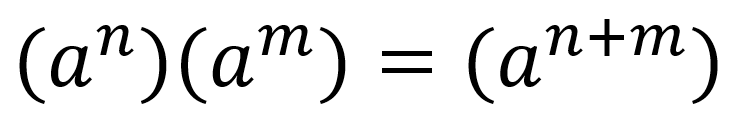
División de potencias con la misma base
Si se desean dividir dos potencias con la misma base, el resultado es una potencia con la misma base y la resta de los exponentes, por ejemplo:
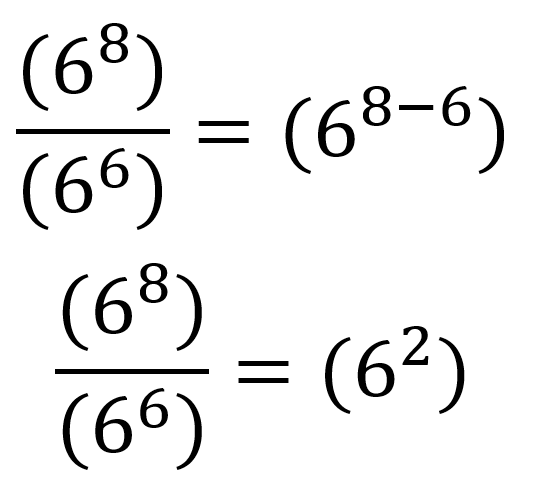
De forma general la división de potencias de misma base se escribe como:
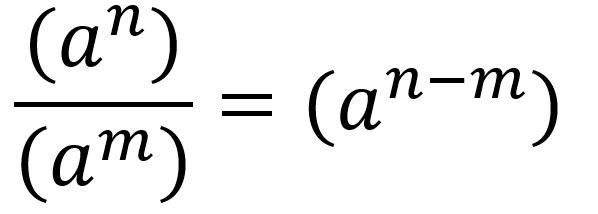
Potencia de una potencia
Una potencia puede elevarse a otra potencia y matemáticamente parece díficil de resolver sin embargo utilizando esta propiedad es muy sencillo hacerlo.
Cuando una potencia se eleva a otra potencia se deben multiplicar los exponentes y mantener la misma base, por ejemplo:
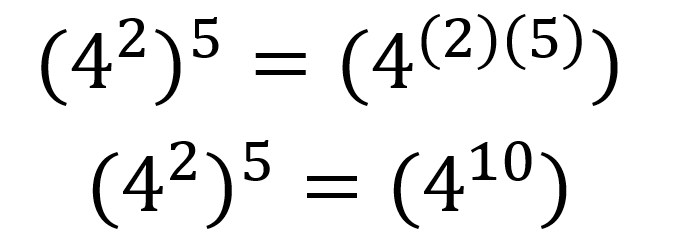
Le expresión general que describe esta propiedad es:
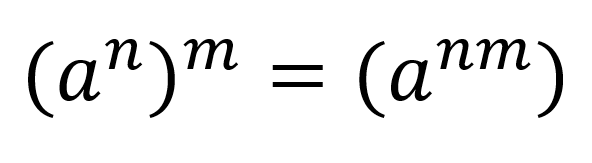
Producto de potencias con el mismo exponente
Si dos potencias tienen el mismo exponente pero diferente base, se deben multiplicar las bases y elevar al exponente en común, por ejemplo:
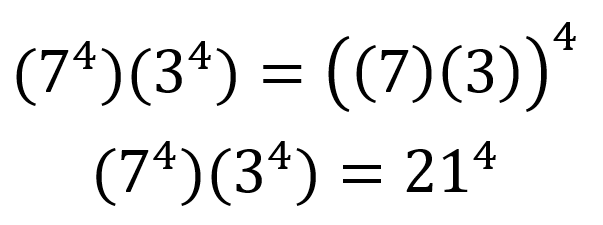
Esta multiplicación, en forma general se puede escribir como:
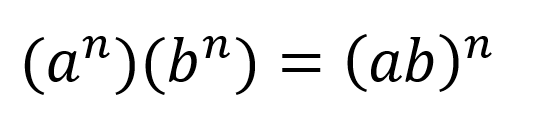
División de potencias con el mismo exponente
Si dos potencias tienen el mismo exponente pero diferente base, se deben dividir las bases y elevar al exponente en común, por ejemplo:
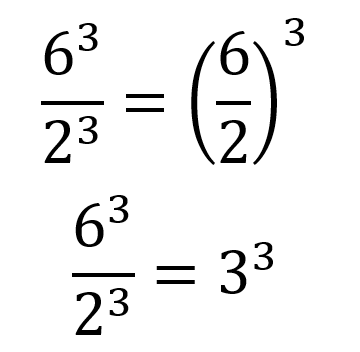
La forma general de escribir esta propiedad es:
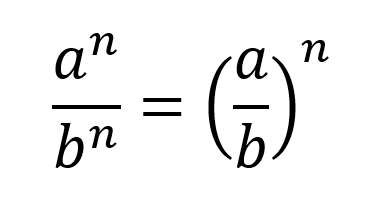
Potenciación con exponentes negativos
Una base con un exponente negativo da como resultado un fraccionario donde el numerador es igual a uno y el denominador es igual a la base con el exponente positivo, por ejemplo.
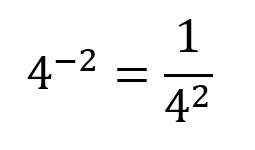
De forma general se puede decir que:
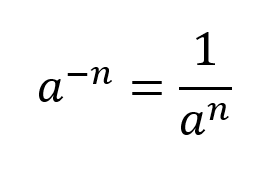
Potenciación en los fraccionarios
Cuando un fraccionario se eleva a una potencia, para resolverse, el numerador se eleva al exponente determinado y el denominador también se eleva al mismo exponente, así:
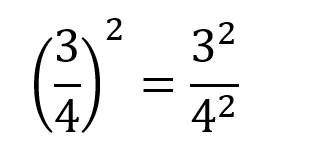
En terminos generales esta propiedad se expresa:
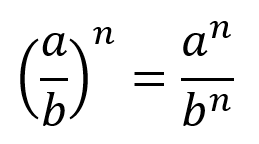
Potenciación en fraccionarios con exponente negativo
Para este caso, cuando se tiene un fraccionario elevado a un exponente negativo, el numerador del fraccionario con exponente negativo pasa como resultado a ser el denominador del fraccionario respuesta pero con el exponente positivo.
Así mismo el que antes era el denominador con exponente negativo, pasa a ser el numerador de la respuesta pero con exponente positivo. Ejemplo:
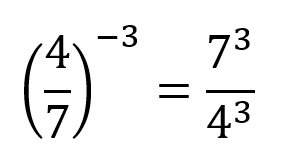
De forma general esta propiedad se expresa:
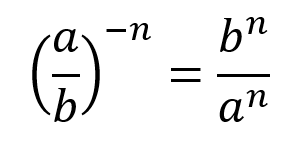
Potencias con exponente fraccionario
Cuando una base tiene un exponente fraccionario esta se puede escribir también en forma de radical, donde el denominador será la raíz y el numerador el exponente, ejemplo:
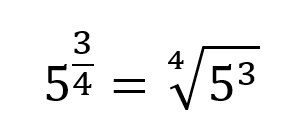
De forma general:
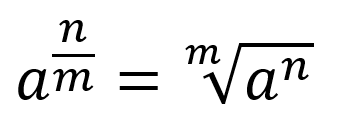
Potencias con exponente fraccionario negativo
En este caso se cumplen las mismas condiciones de exponente fraccionario solo que al ser negativo el exponente se pone el radical positivo en el denominador.
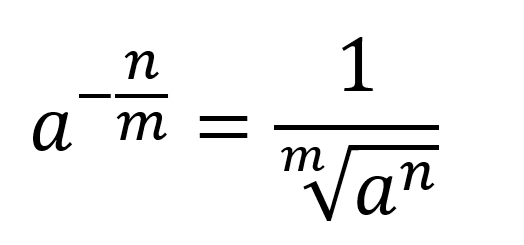
Ley de los signos en la potenciación
La ley de los signos nos explica si el resultado de una operación matemática será positivo o negativo teniendo en cuenta la naturaleza de los números que se están operando.
Si el signo se encuentra dentro del paréntesis
En la potenciación el signo se puede encontrar dentro del paréntesis y para estos casos tenemos dos posibilidades, primero que el exponente sea par o segunda que el exponente sea impar.
Potencias con exponente par
Todas las potencias con exponente par dan como resultado un número positivo, por ejemplo:

Potencias con exponente impar
En las potencias con exponente impar si la base es negativa, tendremos como resultado un número negativo, pero si la base es positiva tendremos como resultado un número positivo, por ejemplo:
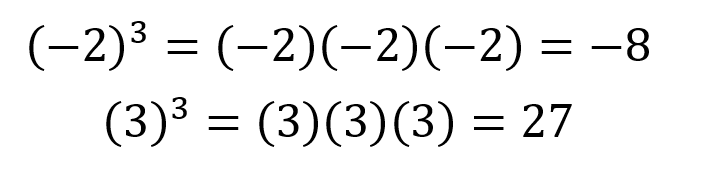
Si el signo se encuentra fuera del paréntesis
Si el signo se encuentra fuera del paréntesis o si no existe ningún paréntesis debemos dejar el resultado igual que el signo, si el signo es positivo (o no hay signo) el resultado será positivo, si el signo es negativo, el resultado será negativo.
Esta condición se debe cumplir independientemente si el exponente es par o impar.
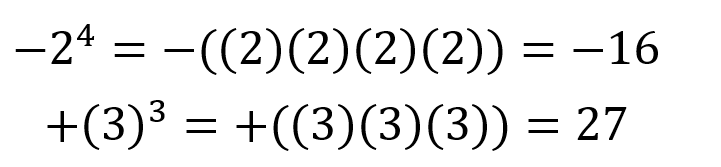
Gráficas
La potenciación es una función matemática que crece con rapidez, aquí puedes ver el comportamiento de los dos principales exponentes.
Gráfica de x al cuadrado
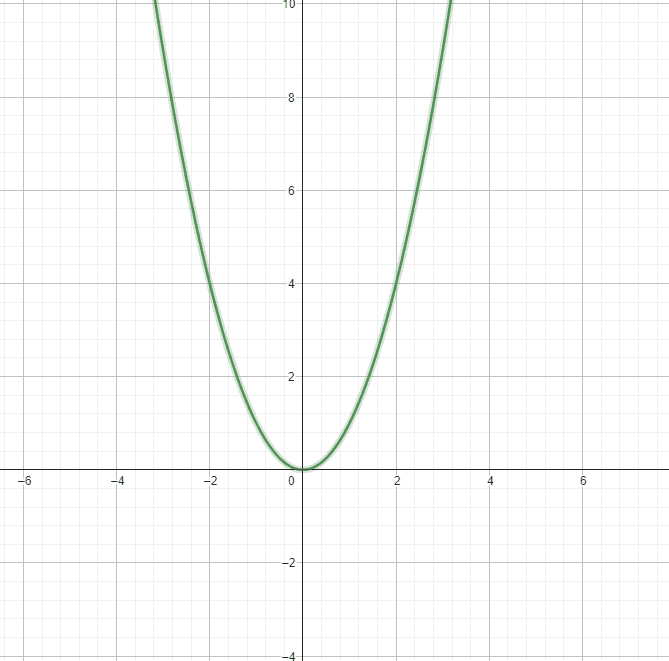
Gráfica de x al cubo
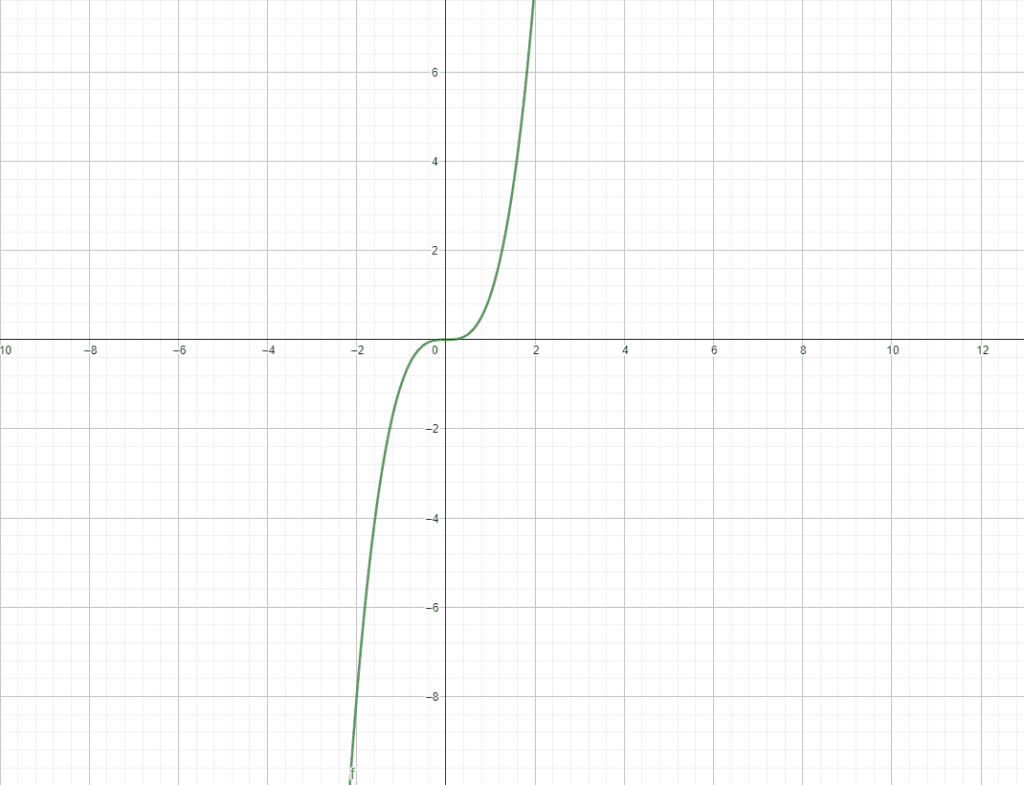
¿Cómo referenciarnos?
Munévar, R. (S.F) Ecuación de Arrhenius. ecuacionde.com. Recuperado el día (fecha en la que nos consultas) de https://ecuacionde.com/potenciacion
Recuerda que si tienes dudas frente a este tema puedes dejar tu pregunta en los comentarios o en nuestra página de contacto
Gracias por visitar nuestra página web.