La ley de los signos o regla de los signos como se conoce en alguna bibliografía permite determinar el signo de un resultado final después de realizar operaciones con números reales.
Las operaciones donde se puede utilizar la ley de los signos son las sumas, restas, multiplicaciones, divisiones, potenciaciones y otras.
Tabla de contenidos
¿Cómo funciona la ley de los signos?
A través de una serie de reglas o normas se establecerá el comportamiento que tendrán los signos a medida que se realicen las operaciones matemáticas, la ley de los signos asigna a los números un (+) si son positivos, o un signo menos (-) si son negativos.
Los números positivos pueden escribirse con el signo más (+) antes del valor pero no es obligatorio, si un número no tiene signo se asume que es positivo, por ejemplo +8 = 8 cualquiera de las dos formas es válida en la escritura.
¿Cuál es la importancia de la ley de los signos?
Debido al amplio uso de las operaciones matemáticas dentro de la cotidianidad de la humanidad la importancia de la correcta aplicación de la ley de signos permite tomar decisiones que pueden llegar a ser vitales.
Por ejemplo si se quisiera realizar una inversión en una potencial empresa y esta presenta sus resultados financieros pero por un error de signos dice que en este momento su balance es de – 450 000 dólares todos los posibles inversionistas se abstendrían de realizar la inversión porque el signo negativo muestra que la empresa está en pérdidas.
¿Cómo se aplica?
Dependiendo de la operación matemática que se quiera realizar se establecen las reglas con las cuales funciona la ley de este modo tenemos:
¿Qué es SVM en la ley de los signos?
En algunas operaciones matemáticas la regla de los signos indica que se debe dejar el signo del valor mayor (SVM) entre dos números, esto significa que se deben evaluar los valores absolutos de los dos números involucrados en la operación y el signo que tenga el número con mayor valor absoluto será el signo del resultado, tranquilo en unos momentos te mostraremos en qué casos se utiliza esto con varios ejemplos.
Ley de los signos en la suma
Cuando se realizan operaciones de suma con números reales, se deben seguir las siguientes reglas:
Regla # 1 para la suma
Si los dos números a sumar son positivos, es decir que ambos son mayores que cero entonces se suman sus valores y se mantiene el signo positivo.
Ejemplo:
7+8 = 15
12+4=16
20+30=50
Regla # 2 para la suma
Si los dos números a sumar son negativos, es decir que ambos son menores que cero entonces se suman sus valores y se mantiene el signo negativo.
Ejemplo:
-25+(-12) = -37
-6 + (-7) = -13
-18 + (-9) = -27
Regla # 3 para la suma
Si se suma un número positivo con uno negativo, o al revés si se suma un número negativo con uno positivo se deben restar el de mayor magnitud con el de menor magnitud y se deja el signo del SVM es decir del que tenga una mayor magnitud.
Ejemplo:
-14+4 = -10
En este caso se restan 14-4= 10 , pero como el número de mayor valor absoluto SVM es -14 se debe dejar ese signo, en este caso es negativo por lo que la respuesta final es -10.
15 + (-10) = 5
En este caso se restan 15-10= 5 , el número de mayor valor absoluto SVM es +15 se debe dejar ese signo, en este caso es positivo por lo que la respuesta final es +5 o 5.
8+(-12) = -4
En este caso se restan 12-8= 4 , pero como el número de mayor valor absoluto SVM es -12 se debe dejar ese signo, en este caso es negativo por lo que la respuesta final es -4.
Resumen en la suma
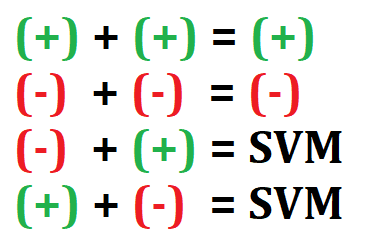
Ley de los signos en la resta
Cuando se tiene una resta se debe cambiar el signo del sustraendo (recuerda que si se tiene a–b entonces a es el minuendo y b es el sustraendo) luego de cambiar el signo se suman los números de acuerdo con el procedimiento y con las mismas reglas de la suma.
Ejemplo 1 ley de signos en la resta
Se quieren restar los números 10 y 7 entonces lo primero es cambiar el signo del sustraendo y hacer la suma, de este modo la operación quedaría:
10-7
10+(-7) = 3
En este caso el número de mayor valor absoluto SVM es +10 entonces se debe dejar ese signo, en este caso es positivo por lo que la respuesta final es +3 o 3.
Ejemplo 2 ley de signos en la resta
Se quieren restar los números 12 y -8 entonces lo primero es cambiar el signo del sustraendo y hacer la suma de este modo la operación quedaría:
12 – (-8)
12 + (8) = 20
Como ambos números eran positivos el resultado se mantiene positivo, la respuesta final es 20 o +20.
Ejemplo 3 ley de signos en la resta
Se quieren restar los números -1 y -7 entonces lo primero es cambiar el signo del sustraendo y hacer la suma de este modo la operación quedaría:
-1 – (-7)
-1+7 = 6
En este caso el número de mayor valor absoluto SVM es +7 entonces se debe dejar ese signo, en este caso es positivo por lo que la respuesta final es +6 o 6.
Resumen en la resta
Recordemos que en la resta se cambia el signo del sustraendo y se hace el mismo procedimiento que la suma por lo tanto el resumen quedaría igual que el de la suma:
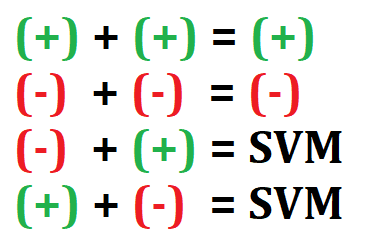
Ley de los signos en la multiplicación
Las reglas de la ley de los signos en la multiplicación es tal vez una de las más conocidas por todos los estudiantes, estas son:
- Si se multiplican dos números con signo positivo (+) el resultado tendrá el signo positivo (+)
- Si se multiplican dos números con signo negativo (-) el resultado tendrá el signo positivo (+)
- Si se multiplican dos números y uno tiene signo positivo (+) y el otro negativo (-) el resultado será negativo (-)
En otras palabras si se multiplican dos números y estos tienen el mismo signo el resultado será positivo de lo contrario el resultado será negativo.
Ejemplos:
20 x 3 = 60
-15 x 2 = -30
4 x -7 = -28
-6 x – 12 = 72
Resumen en la multiplicación
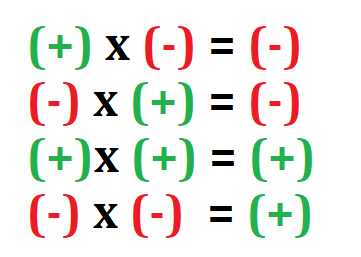
Ley de los signos en la división
Las reglas de la ley de los signos en la división son iguales a los de la multiplicación, estas son:
- Si se dividen dos números con signo positivo (+) el resultado tendrá el signo positivo (+)
- Si se dividen dos números con signo negativo (-) el resultado tendrá el signo positivo (+)v
- Si se dividen dos números y uno tiene signo positivo (+) y el otro negativo (-) el resultado será negativo (-)
En otras palabras si se dividen dos números y estos tienen el mismo signo el resultado será positivo de lo contrario el resultado será negativo.
Ejemplos:
21 / 3 = 7
-16 / 2 = -8
4 /-4 = -1
-6 /- 12 = 0,5
Resumen en la división
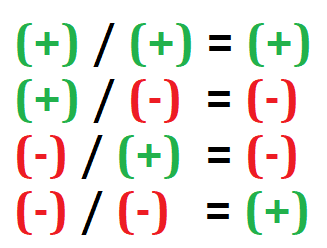
Ley de los signos en la potenciación
Para la potenciación el signo del resultado depende del signo de la base y el exponente, teniendo eso en cuenta se tienen las siguientes reglas:
- Independientemente del signo de la base todas las potencias con exponente par dan un resultado positivo
- Independientemente del signo de la base todas las potencias con exponente impar dan como resultado el mismo signo de la base.
Ejemplo:
-32 = 9
44=256
-23=-8
-24=16
Simplificación de paréntesis
Cuando se tienen paréntesis dentro de las operaciones es importante conocer las siguientes reglas:
- Siempre se resuelven primero los paréntesis.
- Si dos signos queda uno seguido del otro se debe aplicar la regla de la multiplicación.
- Si un signo está detrás de un paréntesis este afecta a todos los elementos dentro del mismo.
Ejemplo 1 simplificación de paréntesis
7-(-3+8)
Lo primero que debemos hacer es resolver lo que se encuentre dentro del paréntesis
7-(+5)
Hay dos signos seguidos el (-) y el (+) por lo que los multiplicamos, recordemos que si son diferentes el resultado es negativo por lo que se reduce a:
7-5
2
El resultado en este caso es 2.
Ejemplo 2 simplificación de paréntesis
-(8x(3-6))
Resolvemos primero lo del paréntesis más pequeño
-(8x(-3))
Luego realizamos la multiplicación
-(-24)
Como quedan dos signos seguidos realizamos la multiplicación de estos, dos signos iguales al multiplicarse se tiene como resultado un valor positivo.
+24
El resultado en este caso es 24.
Si quieres conocer más información al respecto y conocer un poco más de la jerarquía de las operaciones te invitamos a seguir consultando la información en nuestra página.

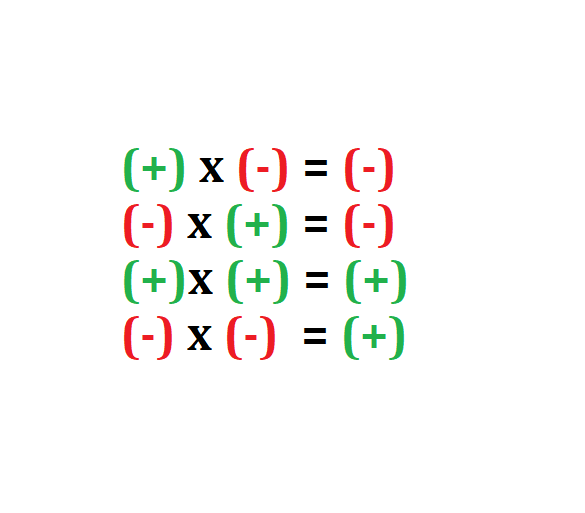
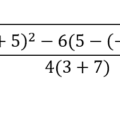
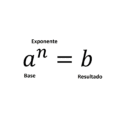
okei
pues entonces hubo una ambiguedad por parte de mis profesores y yo como colega también cometí éste error…
gracias por enfatizarlo apartir de los indicadores lógicos = jerarquía de signos..
a repasar de nuevo éste tema
necesito una aclaración en cuanto a la ley de los signos, un tema que hace años yo ya sé pero una vez más quiero que me afirmes con éste ejemplo de in canal de YouTube, el fulano es @IngEDarwin, según él dice con éste reto ➡️ -3^2 + 9
el signo negativo no acompaña al tres elevado al cuadrado
por ello solo se multiplica por su potencia, dando entender que éste signo no afecta a la base,
por tanto al resolverlo le queda así :
-9 + 9 = 0
cuando estudié se me dijo que todo número acompañado con signo negativo es un número negativo y si éste está elevado a una potencia cuadrada dará un resultado positivo o si éste está elevado a una potencia cúbica dará resultado negativo
entonces, según su reto sería :
-3^2 + 9 = -3 × -3 + 9 = 9 + 9 = 18
Hola Omar, efectivamente cuando se tiene -3^2 por orden de jerarquía queda -(3×3) es decir -9, diferente si se escribiera (-3)^2 que sería (-3)x(-3) = 9 en este caso el youtuber está en lo correcto.