A medida que la humanidad fue utilizando los números para sus actividades cotidianas fue necesario hacer divisiones lo que llevó a la creación de la fracción.
Posteriormente la fracción también se conoció como número fraccionario, estos números pertenecen al conjunto de los números racionales.
Tabla de contenidos
¿Qué es una fracción?
Una fracción o un número fraccionario es la expresión matemática de una cantidad dividida entre otra cantidad.
En la práctica una fracción representa las partes de un todo.

¿De dónde viene la palabra fracción?
El estudio de las fracciones viene desde hace varios siglos, inicialmente en el idioma latín se decía fractio a la acción de romper.
La representación de una división es la ruptura de la unidad en varias partes, de allí los matemáticos adoptaron la palabra fractio para definir a una cantidad dividida en otra.
Tiempo después con el surgimiento de los nuevos idiomas, el español modificó la palabra a como se conoce hoy en día fracción o fraccionario.
¿Cómo se escribe una fracción?
Hay principalmente dos maneras de hacerlo, ambas formas tienen las mismas partes.
La primera es la forma horizontal donde los términos mantienen un mismo nivel:
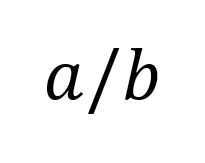
La segunda forma es vertical donde los términos se encuentran uno sobre el otro:
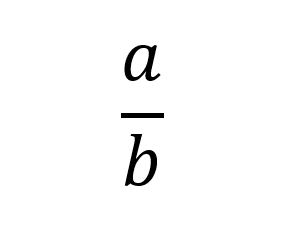
¿Cuáles son las partes o términos de una fracción?
Todas las fracciones se componen de tres partes:
- El número de la parte superior (o izquierda en la representación horizontal) es conocido como el numerador y representa la cantidad de partes que tenemos.
- El número de la parte inferior (o derecha en la representación horizontal) es conocido como el denominador y representa la cantidad de partes en las que hemos dividido la unidad.
- Línea divisoria o línea diagonal es la separación entre el numerador y el denominador.
Términos en la escritura horizontal

en la escritura vertical
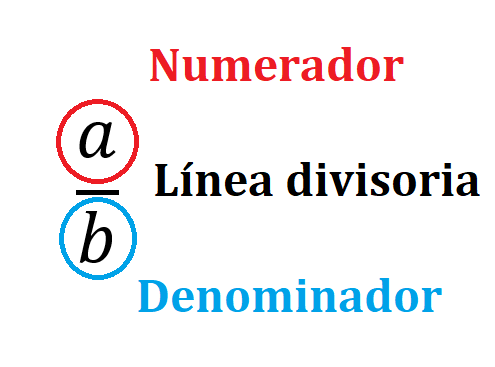
Ambas formas de escritura son totalmente válidas y equivalentes entre sí, en ambas formas aparece el numerador, el denominador y la línea divisoria.
¿Cómo se lee una fracción?
La lectura de la fracción se hace de forma muy sencilla, lo primero que se debe hacer es leer el numerador de forma normal y luego el denominador de acuerdo con las tablas que se presentarán a continuación:
Lectura de numerador
| Número | Lectura | Número | Lectura |
| 1 | Un | 26 | Veintiséis |
| 2 | Dos | 27 | Veintisiete |
| 3 | Tres | 28 | Veintiocho |
| 4 | Cuatro | 29 | Veintinueve |
| 5 | Cinco | 30 | Treinta |
| 6 | Seis | 31 | Treinta y uno |
| 7 | Siete | 32 | Treinta y dos |
| 8 | Ocho | 33 | Treinta y tres |
| 9 | Nueve | 34 | Treinta y cuatro |
| 10 | Diez | 35 | Treinta y cinco |
| 11 | Once | 36 | Treinta y seis |
| 12 | Doce | 37 | Treinta y siete |
| 13 | Trece | 38 | Treinta y ocho |
| 14 | Catorce | 39 | Treinta y nueve |
| 15 | Quince | 40 | Cuarenta |
| 16 | Dieciséis | 41 | Cuarenta y uno |
| 17 | Diecisiete | 42 | Cuarenta y dos |
| 18 | Dieciocho | 43 | Cuarenta y tres |
| 19 | Diecinueve | 44 | Cuarenta y cuatro |
| 20 | Veinte | 45 | Cuarenta y cinco |
| 21 | Veintiuno | 46 | Cuarenta y seis |
| 22 | Veintidós | 47 | Cuarenta y siete |
| 23 | Veintitrés | 48 | Cuarenta y ocho |
| 24 | Veinticuatro | 49 | Cuarenta y nueve |
| 25 | Veinticinco | 50 | Cincuenta |
Lectura de denominador
Después del número 11 se le agrega el sufijo «avos» para indicar que estamos hablando de una fracción.
| Número | Lectura | Número | Lectura |
| 1 | Entero | 26 | Veintiseisavos |
| 2 | Medios | 27 | Veintisieteavos |
| 3 | Tercios | 28 | Veintiochoavos |
| 4 | Cuartos | 29 | Veintinueveavos |
| 5 | Quintos | 30 | Treintavos |
| 6 | Sextos | 31 | Treinta y unavos |
| 7 | Séptimos | 32 | Treinta y dosavos |
| 8 | Octavos | 33 | Treinta y tresavos |
| 9 | Novenos | 34 | Treinta y cuatroavos |
| 10 | Decimos | 35 | Treinta y cincoavos |
| 11 | Onceavos | 36 | Treinta y seisavos |
| 12 | Doceavos | 37 | Treinta y sieteavos |
| 13 | Treceavos | 38 | Treinta y ochoavos |
| 14 | Catorceavos | 39 | Treinta y nueveavos |
| 15 | Quinceavos | 40 | Cuarentavos |
| 16 | Dieciseisavos | 41 | Cuarenta y unavos |
| 17 | Diecisieteavos | 42 | Cuarenta y dosavos |
| 18 | Dieciochoavos | 43 | Cuarenta y tresavos |
| 19 | Diecinueveavos | 44 | Cuarenta y cuatroavos |
| 20 | Veinteavos | 45 | Cuarenta y cincoavos |
| 21 | Veintiunavos | 46 | Cuarenta y seisavos |
| 22 | Veintidosavos | 47 | Cuarenta y sieteavos |
| 23 | Veintitresavos | 48 | Cuarenta y ochoavos |
| 24 | Veinticuatroavos | 49 | Cuarenta y nueveavos |
| 25 | Veinticincoavos | 50 | Cincuentavos |
Si el denominador es un múltiplo de 10 tenemos:
100: Centésimo
1000: Milésimo
10 000: Diez milésimo
100 000: Cien milésimo
1 000 000: Millonésimo
10 000 000: Diez millonésimo
Nota: si la fracción es negativa simplemente se agrega la palabra «menos» antes de la lectura.
Teniendo esto en cuenta vamos a ver varios ejemplos de cómo leer una fracción:
| Fracción | ¿Cómo se lee la fracción? |
|---|---|
| 1/2 | Un medio |
| 7/13 | Siete treceavos |
| -8/7 | Menos ocho séptimos |
| 41/43 | Cuarenta y un cuarenta y tresavos |
| 29/1 | Veintinueve enteros |
| -32/12 | Menos treinta y dos doceavos |
| -9/50 | Menos nueve cincuentavos |
| 6/3 | Seis tercios |
| 20/8 | Veinte octavos |
| 30/30 | Treinta treintavos |
| 43/1 000 000 | Cuarenta y tres millonésimos |
¿Cómo se representan las fracciones?
Existen varias formas de representar a los números racionales o a las fracciones, dependiendo de la actividad que se esté realizando es posible hacerlo de una forma u otra para facilidad y manejo de las cantidades.
Representación gráfica de las fracciones
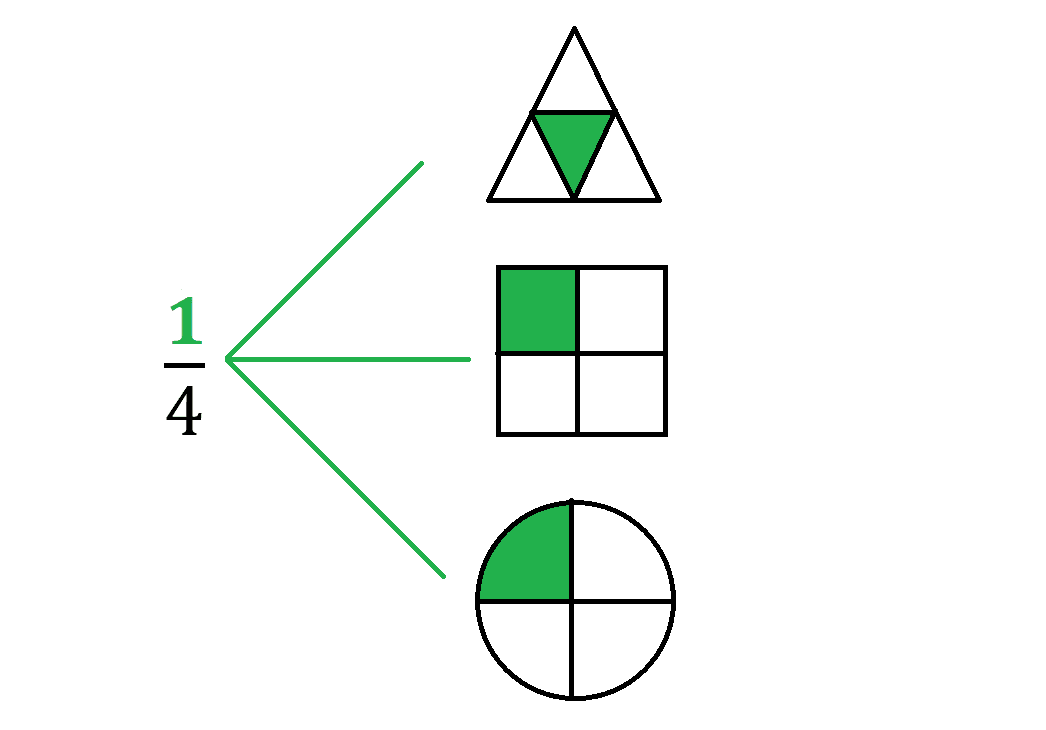
Esta es una de las formas más sencillas de representar una fracción, lo que se hace es dibujar una unidad y dividirlo entre la cantidad de partes que indica el denominador y luego seleccionar la cantidad de partes que indica el numerador, por ejemplo:
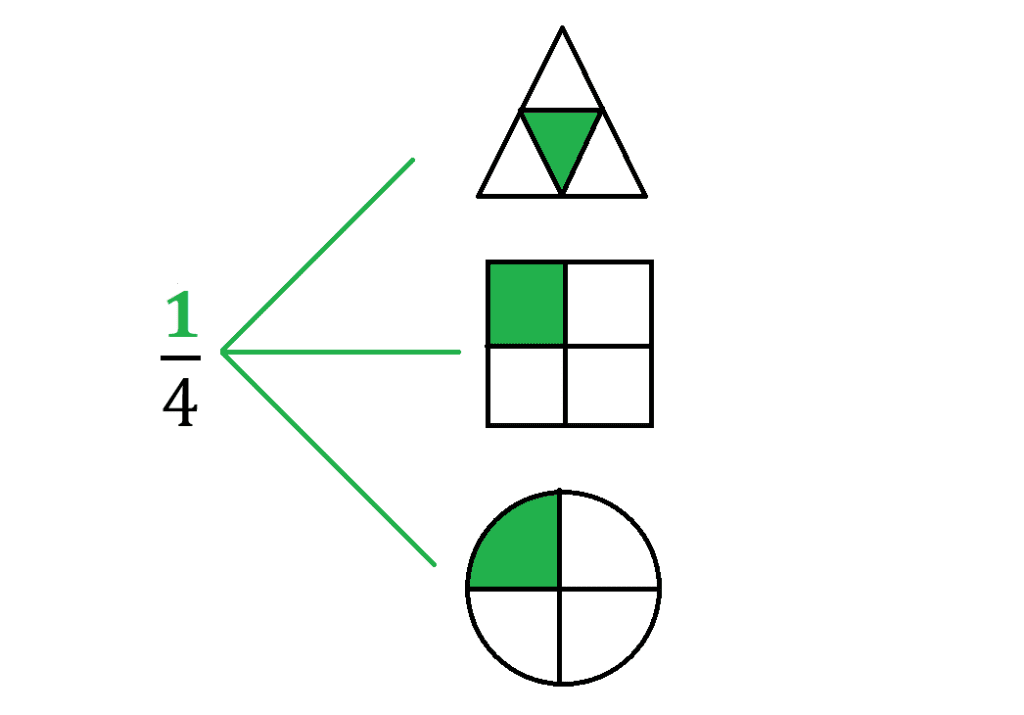
En este caso el fraccionario 1/4 significa que una unidad (una figura geométrica) se dividió en 4 partes iguales y de esas se seleccionó una.
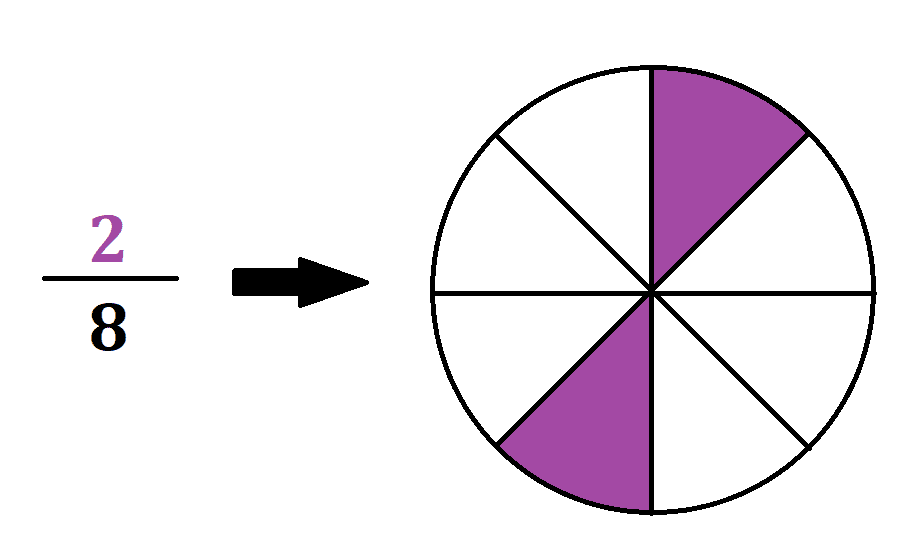
La representación de la fracción 2/8 sería dividiendo la unidad, en este caso el círculo en ocho partes iguales y tomando 2.
¿Cómo se representan si el numerador es mayor que el denominador?
Los casos que hemos visto la cantidad de partes a escoger (el numerador) es menor que las partes en las que fue dividida la unidad, pero ¿Qué pasaría si fuera al contrario?
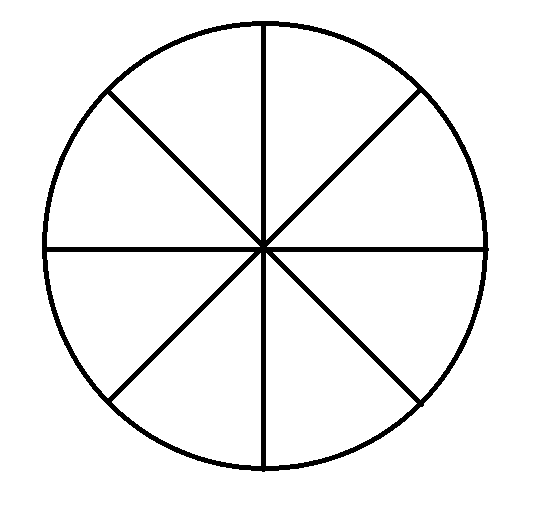
Cuando el numerador es más grande que el denominador debemos utilizar más de una unidad, por ejemplo si queremos representar gráficamente 21/8
El denominador 8 nos dice que la unidad se debe dividir en 8 partes iguales es decir que quedaría:
Pero de acuerdo con el numerador debemos escoger 21 partes y solo tenemos 8, entonces vamos a requerir de más unidades, ahora intentemos con dos:
En este caso vemos que tenemos 16 partes que siguen siendo insuficientes ya que necesitamos 21, por lo que es necesario agregar otra unidad.
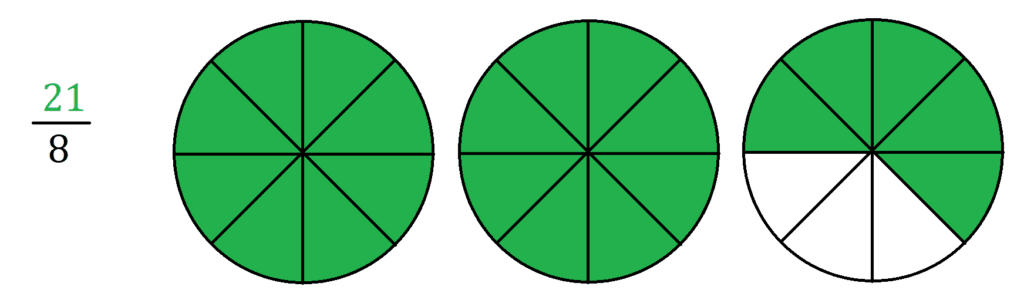
Representación decimal de las fracciones
Al ser una división entre dos números, las fracciones también se pueden representar de forma decimal resolviendo dicha división.
Por ejemplo:
1/2 = 0,5
1/4 = 0,25
7/4 = 1,75
9/8 = 1,125
Representación porcentual de las fracciones
El símbolo de porcentaje % se utiliza para representar las partes de una unidad, es decir representa también lo que es una fracción.
Pasar de porcentaje a fracción
Para escribir un porcentaje en forma de fracción lo único que debe hacerse es dividir el porcentaje entre 100, por ejemplo:
En una comunidad de Toledo de 200 personas el 50% está de acuerdo con una decisión política, ¿Cuántas personas están de acuerdo?
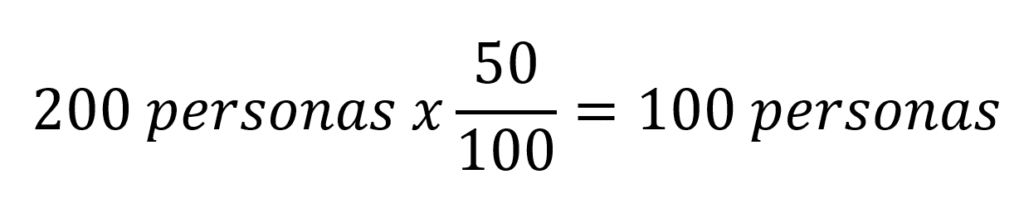
En este caso 100 personas están de acuerdo con la decisión, para convertir el 50% a una fracción simplemente se dividió 50 entre 100 quedando el fraccionario 50/100.
| Porcentaje | Fraccionario | Porcentaje | Fraccionario |
|---|---|---|---|
| 10% | 10/100 | 60% | 60/100 |
| 20% | 20/100 | 70% | 70/100 |
| 30% | 30/100 | 80% | 80/100 |
| 40% | 40/100 | 90% | 90/100 |
| 50% | 50/100 | 100% | 100/100 |
Pasar de decimal a porcentaje
En caso contrario cuando se tiene un decimal y se quiere pasar a porcentaje simplemente se debe multiplicar por 100 y añadir el símbolo %.
Por ejemplo en Madrid 1/4 de las personas utilizan el metro todos los días, ¿Qué porcentaje equivale?
Se resuelve la división de 1/4 = 0,25 y una vez se tiene el decimal se multiplica por 100
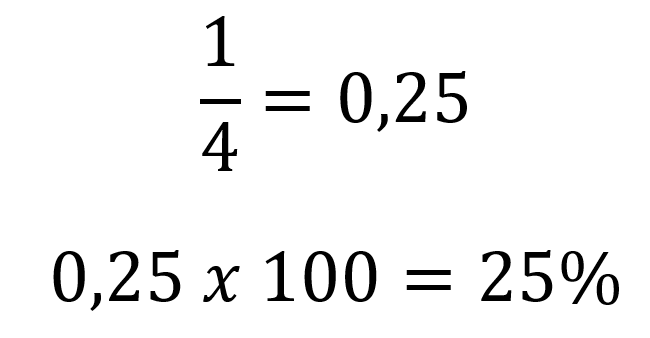
En este caso se puede decir que el 25% de las personas en Madrid utilizan el metro todos los días.
¿Cómo explicar fracciones a un niño?
Muchas veces te habrás preguntado ¿Cómo hago para explicarle a un niño el tema de fracciones? sin embargo es un tema bastante sencillo en el que puedes utilizar elementos que muy probablemente ya tienes en casa.
Lo primero que debes enseñar es a que el niño comprenda el tema del denominador que es en cuántas partes está dividida la unidad.

Por ejemplo a través de un simple rompecabezas de cuatro piezas puedes explicarle qué representa 1/4, 2/4, 3/4 y que la unidad completa representa 4/4.
Una vez el niño domine el concepto de numerador, se procede a que comprenda el concepto del denominador, para ello es importante que pueda hacer las divisiones necesarias en una unidad, el ejemplo más sencillo es el trabajo con una pizza.

A través de esta actividad el niño puede apropiar el concepto de denominador dividiendo la pizza por ejemplo en 2, 4 u 8 partes.
¿Para qué sirven las fracciones en la vida cotidiana?
Son muchos los ejemplos del uso de las fracciones en la vida cotidiana ya que la división de números se ha expandido a diferentes aspectos entre los más comunes tenemos:
Usos de un medio (1/2)
- En los deportes como el fútbol se utiliza el término de medio tiempo para hacer referencia a los primeros 45 minutos del partido.
- En el sector alimenticio se utilizan presentaciones de medio kilogramo para el empaque de algunos productos como el arroz, lentejas, fríjol, entre otros.
- En la cocina se utilizan en algunas ocasiones media naranja para hacer recetas y muchas otras frutas.
Utilidades de un tercio (1/3)
- Cuando se requiere dividir una herencia entre tres personas se dice que a cada uno le correspondió 1/3 de la misma.
- En encuestas cuando se dice que una de cada tres personas prefiere un producto se está hablando de la fracción 1/3.
- En algunos lugares se hace referencia a 1/3 de hora cuando se está hablando de 20 minutos.
Aplicaciones de un cuarto (1/4)
- Otros deportes como el basquetbol dividen los partidos en cuatro tiempos iguales por lo que a cada uno se el conoce como un cuarto de partido.
- También cuando se habla de tiempo un cuarto de hora hace referencia a 15 minutos.
- En algunos países productos como la gasolina se distribuyen en cuartos de galón.
Usos de otras fracciones
Siempre que se tenga una división interna de un conjunto el uso de las fracciones será fundamental, por ejemplo en las elecciones de un país se puede decir que 4/7 de la población prefiere a un candidato.
Cuando se habla de la división demográfica también es completamente válido estipular a través de una fracción que mis ingresos superan al de 9/10 de población.
Entre otros muchísimos casos de aplicación de las fracciones en la vida cotidiana.
Tipos de fracción
Debido a que las fracciones son infinitas por su propia naturaleza de ser un conjunto perteneciente a los números reales se han hecho diferentes clasificaciones de acuerdo a características en común.
Fracciones equivalentes
Las fracciones equivalentes son iguales o representan la misma cantidad pero están escritas de forma diferente, se caracterizan porque tanto el numerador y el denominador de la segunda fracción son múltiplos de la primera.
Por ejemplo las fracciones equivalentes a 3/4 son:
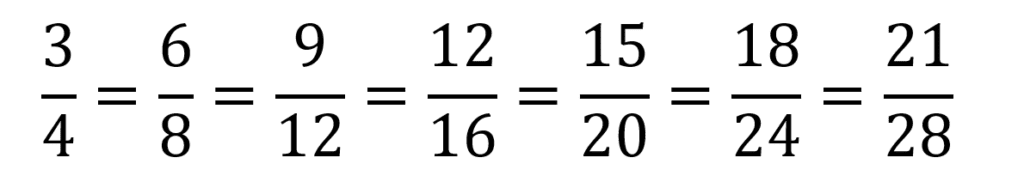
En este caso todas las fracciones son equivalentes ya que su valor en en decimal es de 0,75.
Otro ejemplo de fracciones equivalentes si tomamos como base 7/6 sería:
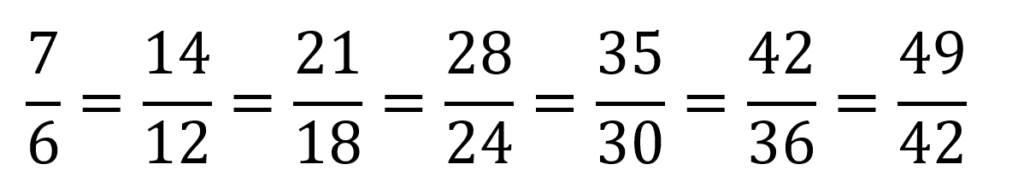
Así mismo todas estas fracciones son equivalentes entre ellas ya que su valor en decimal es de 1,1666…
Fracciones mixtas
Las fracciones mixtas son una mezcla entre las unidades que se escriben como número entero y la parte decimal que se escribe en forma de fracción con la condición de que debe ser menor a uno.
Pasar de decimal a fracción mixta
Por ejemplo si se tiene la fracción 42/10 cuando se pasa a decimal equivale a 4,2 es decir 4 unidades completas y 2/10 que simplificando quedaría escrito como 1/5 obteniéndose:
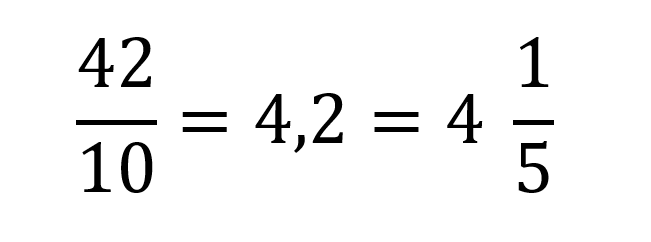
Es decir que 42/10 es exactamente igual a 4,2 y a su vez es exactamente igual a cuatro enteros y 1/5.
Pasar de fracción mixta a decimal
Cuando se tiene una fracción mixta se debe multiplicar las unidades con el denominador y a ese resultado sumarle el numerador.
Una vez se tiene ese resultado la fracción resultante será la suma realizada dividida entre el denominador.
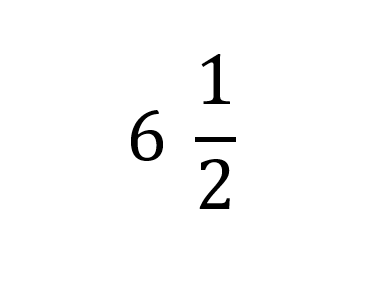
Entonces el procedimiento a realizar es multiplicar las unidades que en este caso son 6 con el denominador que es 2 y sumarle el numerador que es uno, este resultado será el nuevo numerador y se mantiene el denominador que es 2 así:
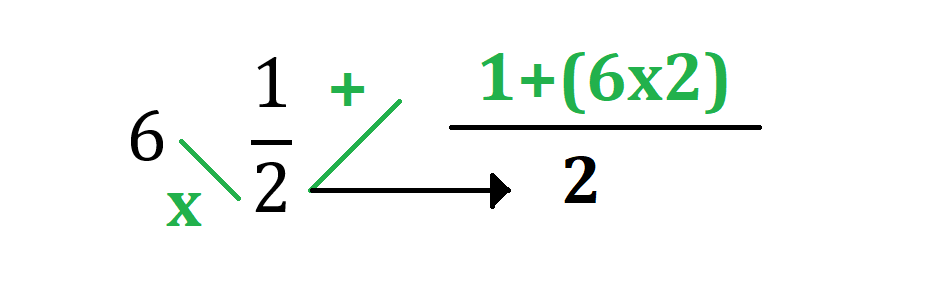
Resolviendo se tiene que:
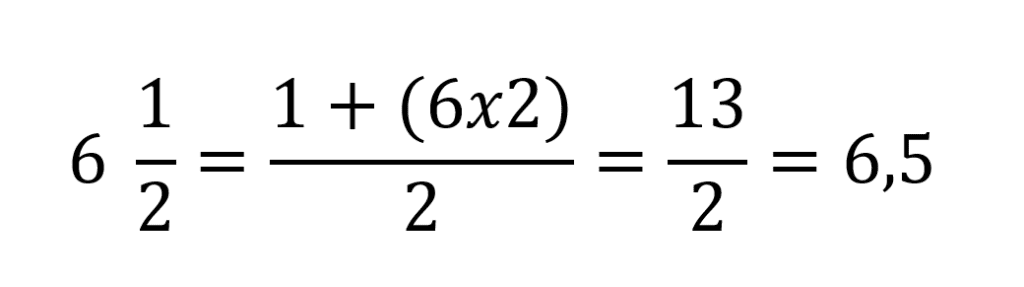
Entonces 6 enteros y un medio es igual a 13/2 que equivale a su vez a 6,5
Fracciones compuestas
Este tipo de fracción hace referencia a que se tiene una fracción mixta en el numerador o en el denominador de una nueva fracción más compleja.
Algunos ejemplos de fracciones compuestas son:
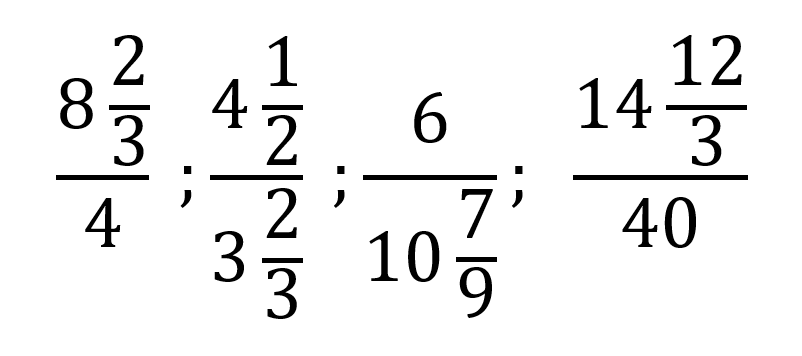
Fracción propia
Las fracciones propias son aquellas donde el numerador es menor que el denominador siempre y cuando ambos sean mayores que cero.
Estos son algunos ejemplos de fracciones propias
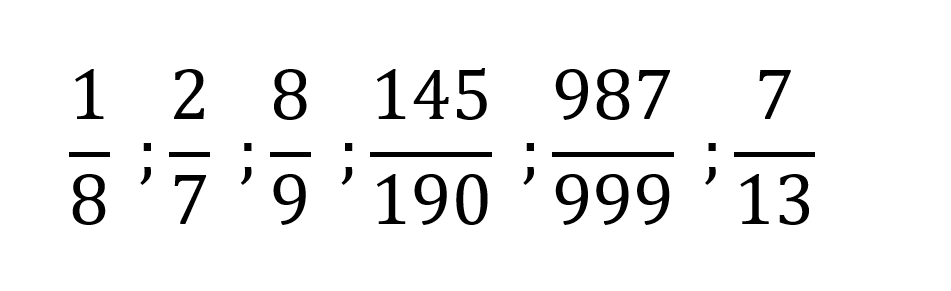
Fracciones impropias
Las fracciones impropias son aquellas donde el numerador es mayor que el denominador siempre y cuando ambos sean mayores que cero.
Estos son algunos ejemplos de fracciones impropias
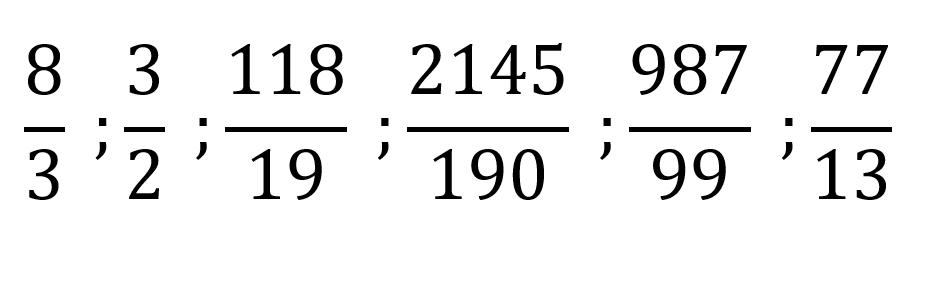
Fracción unitaria
Las fracciones unitarias son aquellas que al resolverse su valor equivale a uno (1) tienen como característica que el numerador y el denominador son iguales.
Estos son algunos ejemplos de fracciones unitarias
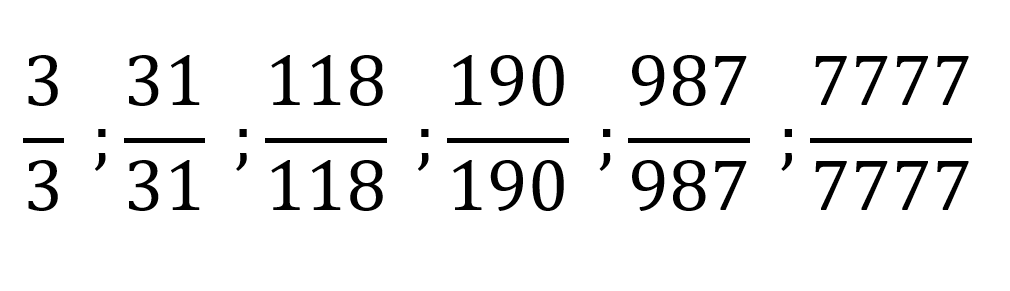
Fracciones homogéneas
Las fracciones homogéneas son aquellas que tienen el mismo denominador, el numerador puede variar.
Estos son algunos ejemplos de fracciones homogéneas:
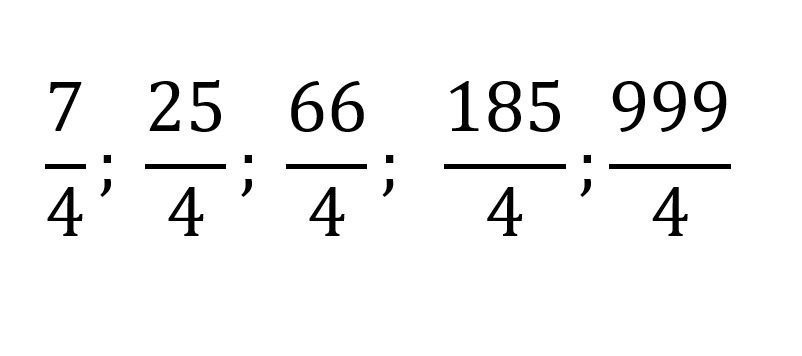
Fracciones heterogéneas
Las fracciones heterogéneas son aquellas que tienen diferente denominador, el valor del numerador no influye en la definición de la heterogeneidad.
Estos son algunos ejemplos de fracciones heterogéneas:
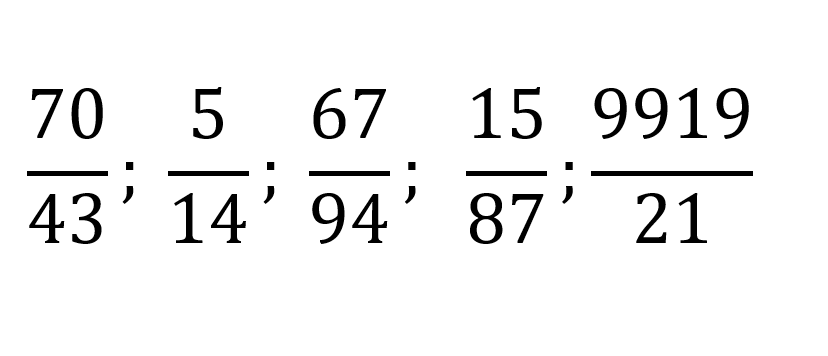
Fracciones irreducibles
Son aquellas fracciones en los que el numerador y el denominador no tienen un divisor en común.
Estos son algunos ejemplos de fracciones irreducibles:
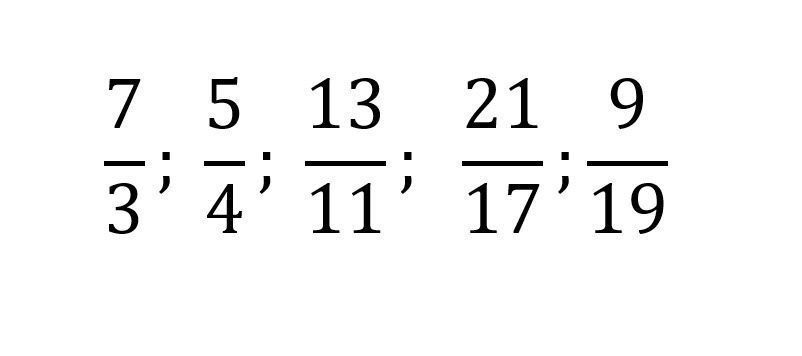
Operaciones matemáticas con fracciones
Las fracciones al ser números racionales están sujetos a ser operados matemáticamente, dentro de esto es posible sumar fraccionarios, restarlos, multiplicarlos, dividirlos y aplicar exponentes
Suma de fracciones
El procedimiento para realizar suma de fracciones depende de si estás son homogéneas o si son heterogéneas, es decir si tienen o no el mismo denominador.
Suma con mismo denominador
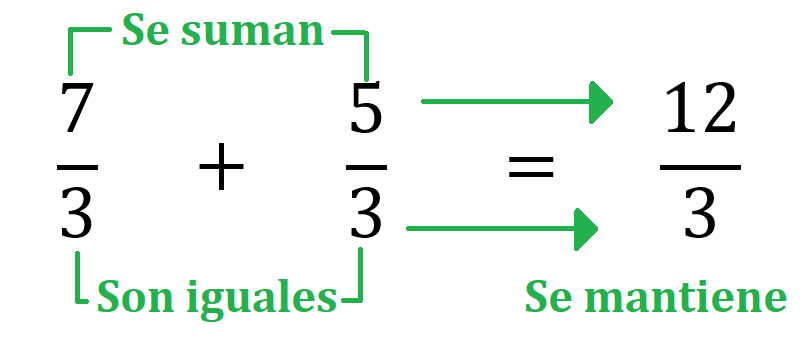
Cuando las fracciones son homogéneas, es decir tienen el mismo denominador, se deben sumar los numeradores y se mantiene el mismo denominador.
Por ejemplo si se quiere sumar 7/3 con 5/3
Otro ejemplo podría ser
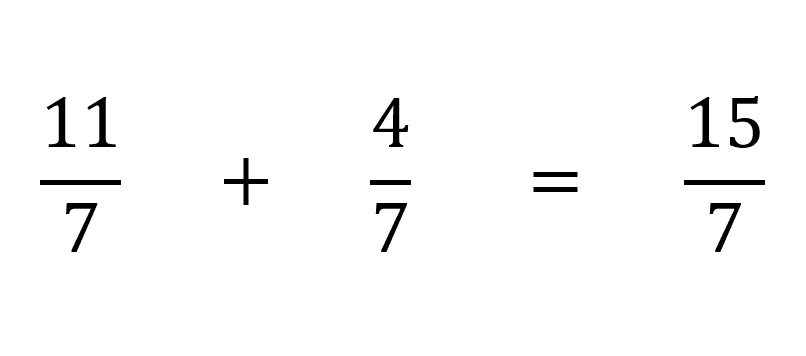
Del mismo modo se mantiene el denominador y se suman los numeradores.
Suma con diferente denominador
Cuando se tienen fracciones con diferente denominador, es decir fracciones heterogéneas el procedimiento para la suma cambia siendo así:
- Se multiplica el numerador del primer fraccionario con el denominador del segundo
- Se multiplica el denominador del primer fraccionario con el numerador del segundo
- Se suma lo obtenido en los pasos 1 y 2, este resultado será el numerador de la respuesta.
- Se multiplican los denominadores de los dos fraccionarios y este resultado será el denominador de la respuesta.
¿Complicado? para nada, vamos a hacer unos ejemplos para que te quede más claro:
Vamos a sumar 11/3 con 4/9:
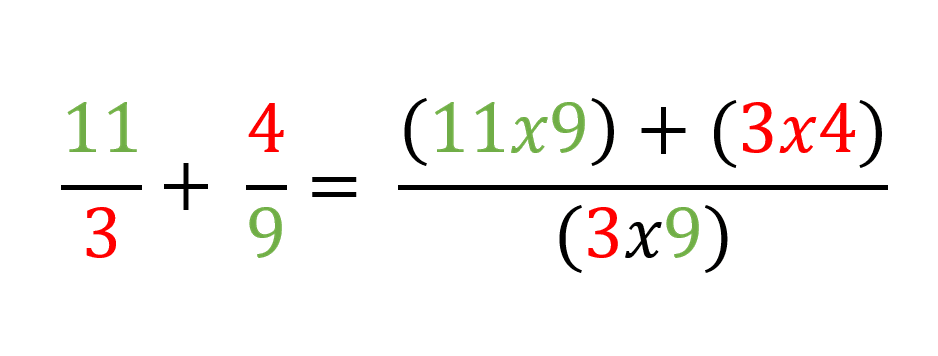
Una vez se tienen las operaciones definidas se procede a solucionar:
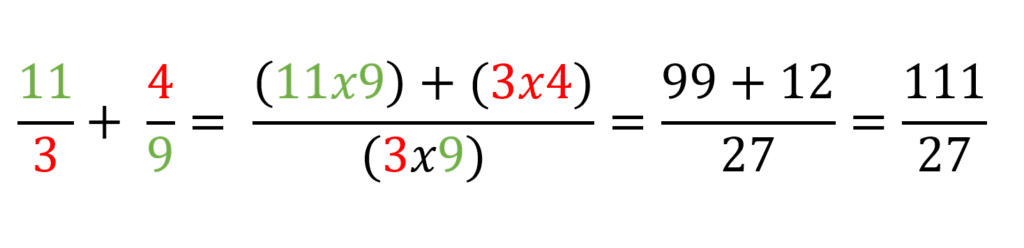
Para que recuerdes una forma sencilla de realizar el orden de las operaciones en la suma de fraccionarios es con el emoji «XD» ya que se debe hacer:
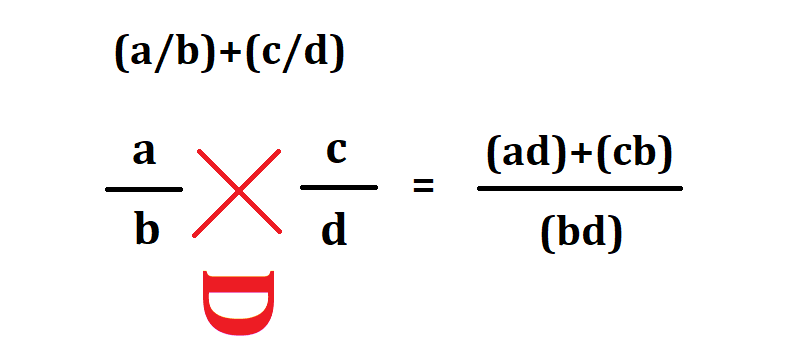
Veamos otro ejemplo, para este caso sumaremos 1/2 + 1/3
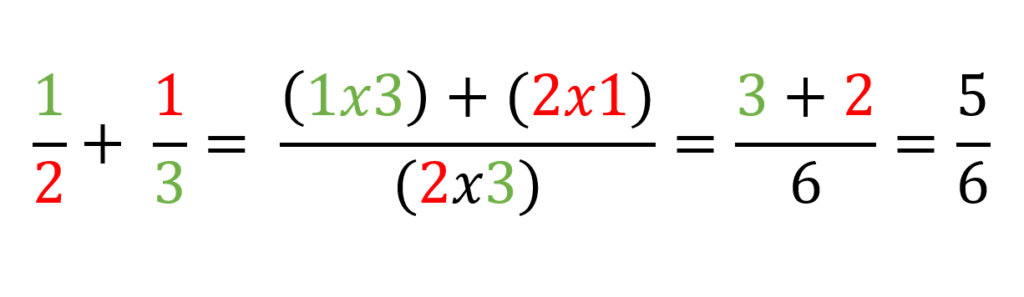
En este caso 1/2 +1/3 equivale a 5/6
Resta de fracciones
La resta de fraccionarios tiene las mismas condiciones que la suma, depende de si las fracciones tienen o no el mismo denominador.
Resta con mismo denominador
Cuando las fracciones son homogéneas, es decir tienen el mismo denominador, se deben restar los numeradores y se mantiene el mismo denominador.
Por ejemplo si se quiere restar 6/3 con 8/3
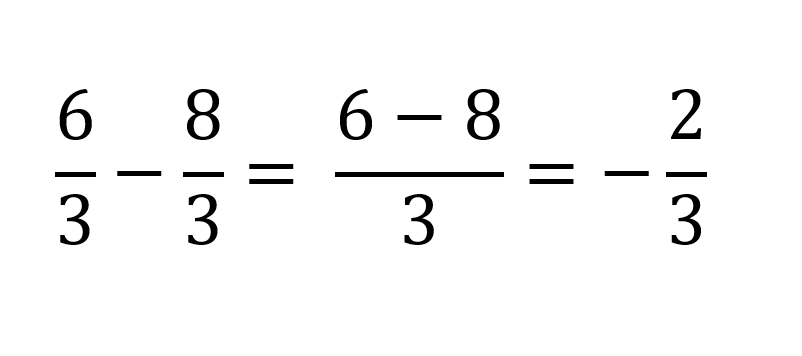
En este caso como la segunda fracción es mayor el resultado queda negativo ya que 6-8 = -2
Otro ejemplo es si se quiere restar 9/7 – 4/7
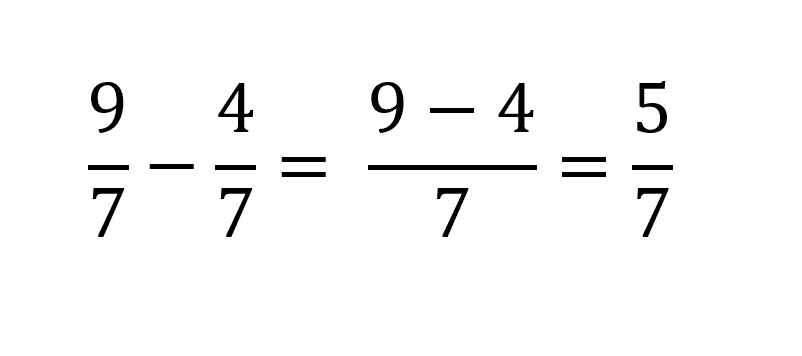
Resta con diferente denominador
Cuando se tienen fracciones con diferente denominador, es decir fracciones heterogéneas el procedimiento para la resta cambia siendo así:
- Se multiplica el numerador del primer fraccionario con el denominador del segundo
- Se multiplica el denominador del primer fraccionario con el numerador del segundo
- Se resta lo obtenido en los pasos 1 y 2, este resultado será el numerador de la respuesta.
- Se multiplican los denominadores de los dos fraccionarios y este resultado será el denominador de la respuesta.
Nuevamente puedes recordar el emoji «XD» pero esta vez con la resta
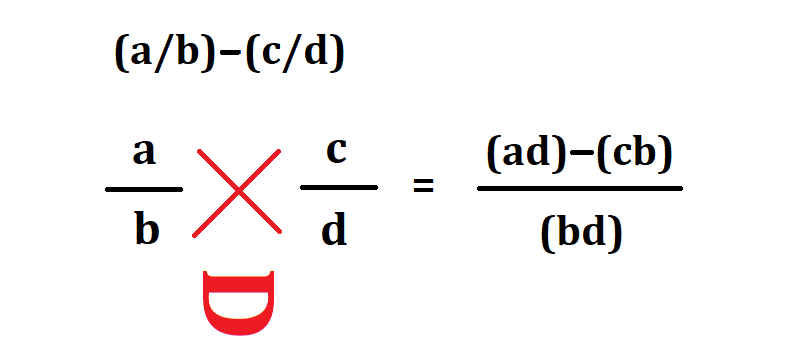
Vamos a realizar el procedimiento para restar 4/5-1/3
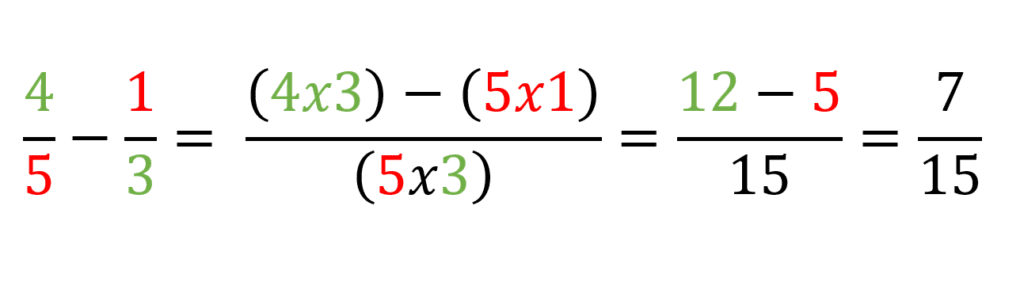
Multiplicación
La multiplicación de fracciones es bastante sencilla, ya que no importa si son homogéneas o heterogéneas, se debe multiplicar numerador con numerador y denominador con denominador, de este modo se obtiene tanto el numerador como el denominador de la respuesta.
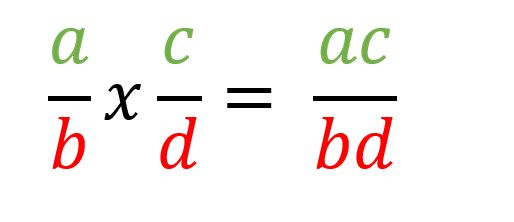
Entonces si se quiere multiplicar por ejemplo 9/5 x 7/11 el procedimiento es:
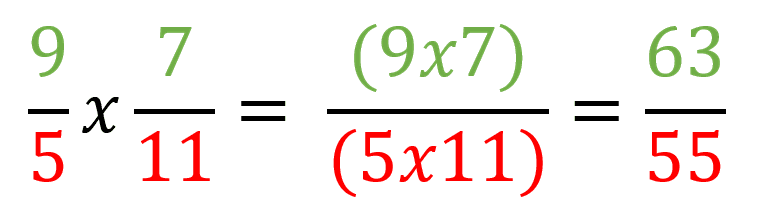
División
La división también es un procedimiento sencillo donde se aplica la conocida ley de la oreja donde se multiplican los extremos y los medios de las fracciones y el resultado de la operación es extremos dividido entre medios.
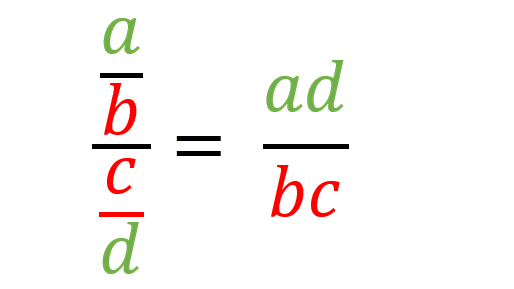
Por ejemplo si se quiere dividir 25/12 entre 1/4 el procedimiento sería:
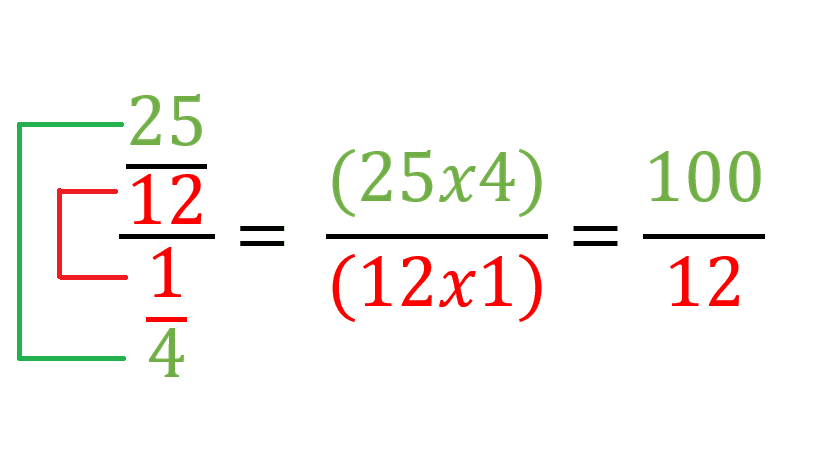
Exponenciación
Para elevar una fracción a cualquier exponente se elevan el numerador y el denominador por separado a dicho exponente.
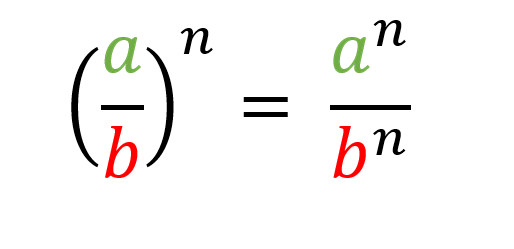
Por ejemplo si se quiere elevar 3/4 al cuadrado el procedimiento es:
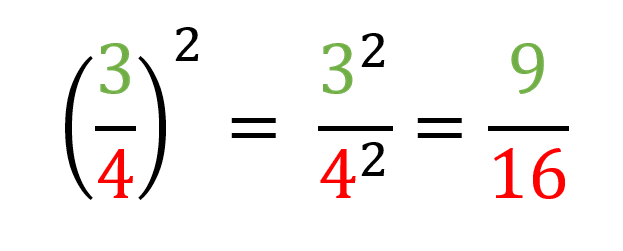
Simplificación
Conociendo que hay fracciones equivalentes y en la búsqueda de simplificar las cifras se recomienda escribir cada expresión en la forma más simple posible, esa forma equivale a la fracción equivalente irreducible donde tanto el numerador y el denominador sean las más cercanas a cero.
Para lograr esto se debe descomponer cada número es sus múltiplos primos empezando con el dos.
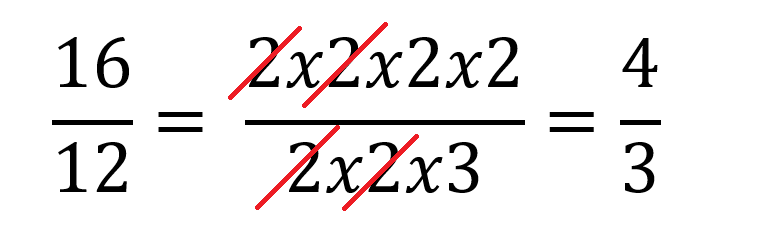
Luego se cancelan los que se repitan tanto en el numerador como en el denominador y se deja el resultado de las operaciones resultantes.