La ecuación de continuidad es un resultado matemático de la ley de conservación de la materia que se puede aplicar cuando se tiene un fluido ideal.
Tabla de contenidos
¿Qué es un fluido ideal?
Para ser considerado un fluido ideal y por ende poder aplicarse la ecuación de continuidad se tienen que tener cuatro características fundamentales:
- Flujo constante: todas las partículas del fluido dentro de la tubería tienen la misma velocidad independientemente del punto en el que se encuentren.
- Flujo irrotacional: el fluido no posee velocidad angular neta, es decir, no existe posibilidad que se presenten remolinos dentro de la tubería.
- Flujo incompresible: esto significa que la densidad del fluido es constante en cualquier condición de presión.
- Flujo no viscoso: se considera que no existe (o al menos es insignificante) la fricción interna de las moléculas del fluido, es decir, la capacidad de resistencia al movimiento tiende a cero.
Demostración de la ecuación de continuidad
Se tiene un fluido ideal que se mueve a través de una tubería tal como se muestra en la figura 1.
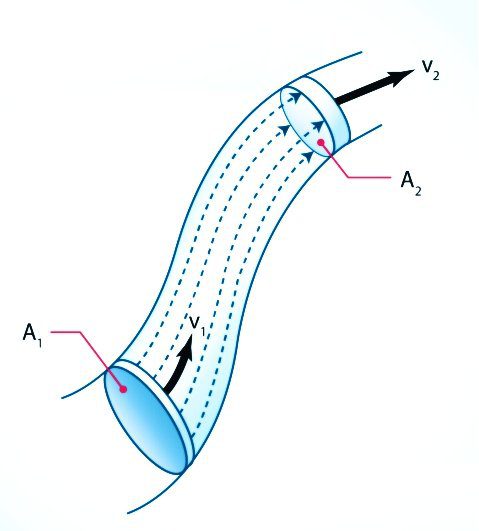
Si no hay pérdidas de fluido por alguna fuga, la cantidad de masa que entra en un determinado intervalo de tiempo es igual a la cantidad de masa que sale. No puede salir más masa de la que está entrando ya que es físicamente imposible, tampoco puede salir menos masa de la que entra porque esto significaría que hay una acumulación dentro de la tubería lo que haría que estallase.
Teniendo esto en cuenta se conoce entonces que caudal de entrada es igual a caudal de salida, representado mediante la ecuación 1:
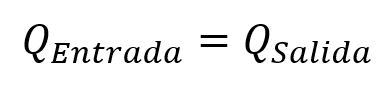
Se conoce que el caudal es la masa que se mueve a través de la tubería en un tiempo determinado, por lo que la ecuación se puede escribir de la forma:
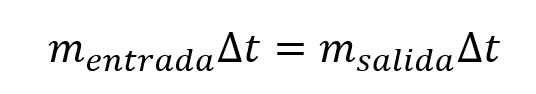
También se conoce que la densidad de un fluido es igual a su masa sobre el volumen que ocupa así:
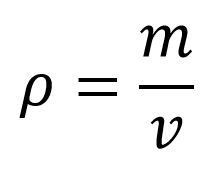
Despejando la masa de la fórmula general de la densidad se tiene que:
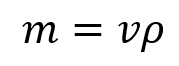
Reemplazando la ecuación 4 en la ecuación 2 se tiene entonces que:
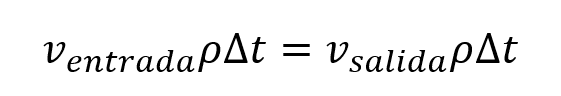
El volumen del agua en un determinado lapso de tiempo corresponde al área transversal de la tubería multiplicado por la distancia (d) que recorre por lo que la ecuación queda transformada en:
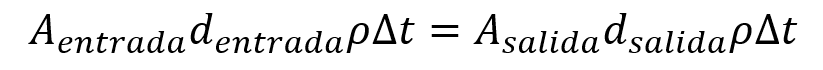
La distancia que recorre un cuerpo en un intervalo de tiempo determinado se conoce como velocidad, así pues la ecuación se transforma en:
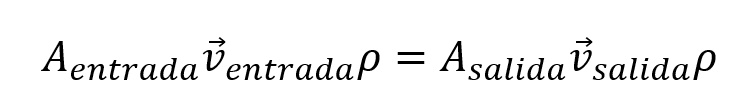
Como el fluido al realizar el recorrido a lo largo de la tubería no sufre cambios de estado, y se está trabajando con fluidos ideales, es decir incompresibles, la densidad del fluido a la entrada de la tubería es igual a la densidad de la salida entonces la ecuación de continuidad se escribe:
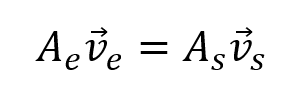
Ejercicios resueltos de la ecuación de continuidad
Existen diferentes preguntas que pueden surgir a partir de la ecuación de continuidad donde básicamente se busca encontrar una incógnita dentro de una situación dada con un fluido, los principales problemas son:
Ejercicio 1. Calcular el caudal que fluye a través de una tubería
Se tiene una tubería circular de radio 10 cm por donde fluye agua con una velocidad de 3 m/s ¿Cuál es el caudal?
Solución

El primer paso es establecer los datos conocidos que para este ejercicio son tanto la velocidad como el diámetro de la tubería (teniendo en cuenta que es una tubería circular).
Se establece la ecuación de continuidad donde se conoce que el caudal de entrada es igual al caudal de salida.
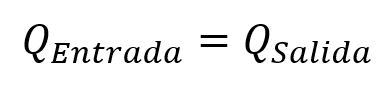
Al tiempo que se tiene la ecuación de continuidad expresada en área por velocidad.
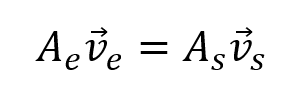
Si unificamos las dos ecuaciones tendríamos que:
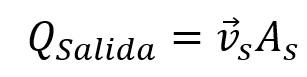
De este modo podemos conocer el caudal ya que la velocidad es un dato conocido y el área se puede conocer a partir del diámetro.
NOTA: en este caso se está utilizando caudal de salida en la ecuación pero también se puede utilizar el caudal de entrada, recordemos que ambos son iguales y que en el ejercicio no se especifica si se está hablando a la entrada o a la salida, simplemente se pide el caudal que es el mismo en cualquier punto.
Recordemos que el área del círculo es igual a pi por el diámetro al cuadrado sobre cuatro y este se debe calcular con las unidades en metros para que sea equivalente en unidades todo el ejercicio.
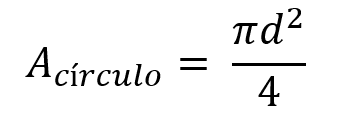
Para este caso el diámetro es de 10 cm lo que equivale a 0,10 metros, la velocidad también se encuentra en metros sobre segundo permitiendo así que se operen las dos magnitudes.
Luego el caudal es:
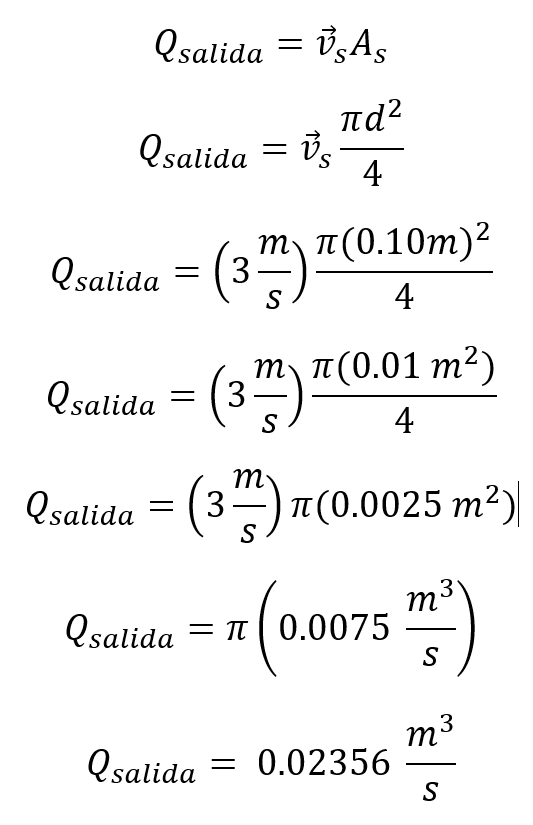
El caudal que pasa por la tubería es de 0.02356 m3/s lo que equivale a 23.56 litros por segundo.
Ejercicio 2. Calcular el diámetro de una tubería por la que fluye un caudal
Por una tubería fluyen 40 litros por segundo de aceite mineral a una velocidad de 5 m/s ¿Cuál es el diámetro de la tubería?

Para solucionar este ejercicio debemos utilizar la ecuación de continuidad igualando el caudal a la velocidad por el área:
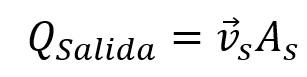
Una vez más recordamos el área del círculo quedando la ecuación convertida en:
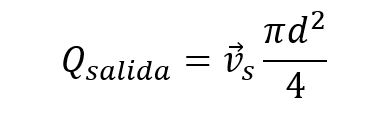
Recordemos que 40 litros por segundo equivalen a 0.04 metros cúbicos por segundo, para así reemplazar los valores conocidos y despejar la única incógnita que es el diámetro.
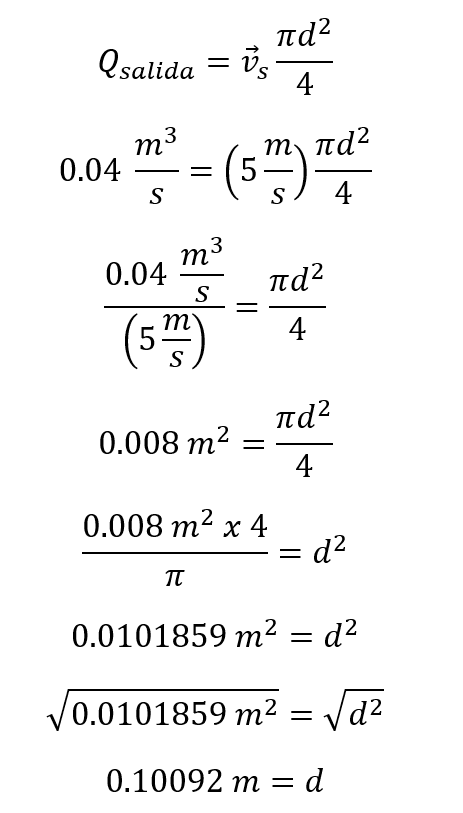
Ejercicio 3. Calcular la velocidad de entrada de una tubería por la que fluye un caudal conociendo los datos de salida.
La velocidad de salida de una tubería cuadrada de lado 50 cm es de 2 m/s, se conoce que dicha tubería tiene un adaptador y una entrada cuadrada de lado 20 cm, ¿Cuál es la velocidad de entrada a la tubería?

Solución
Para solucionar este ejercicio se debe tener en cuenta que la tubería es cuadrada, es decir el área va a cambiar con respecto a los ejercicios anteriores ya que el área del cuadrado es lado por lado.
Inicialmente se plantea la ecuación de continuidad.
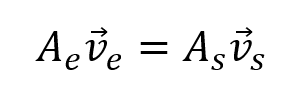
Reemplazando las áreas tanto de entrada como de salida la ecuación de continuidad queda transformada en:
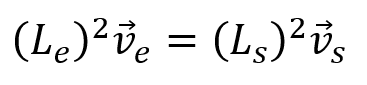
Recordemos que el área de un cuadrado es lado por lado es decir lado al cuadrado, por eso la ecuación toma esa forma. Se reemplazan los datos conocidos sin olvidar que se deben escribir las unidades en el sistema internacional de medidas en este caso el lado de las tuberías se debe escribir en metros.
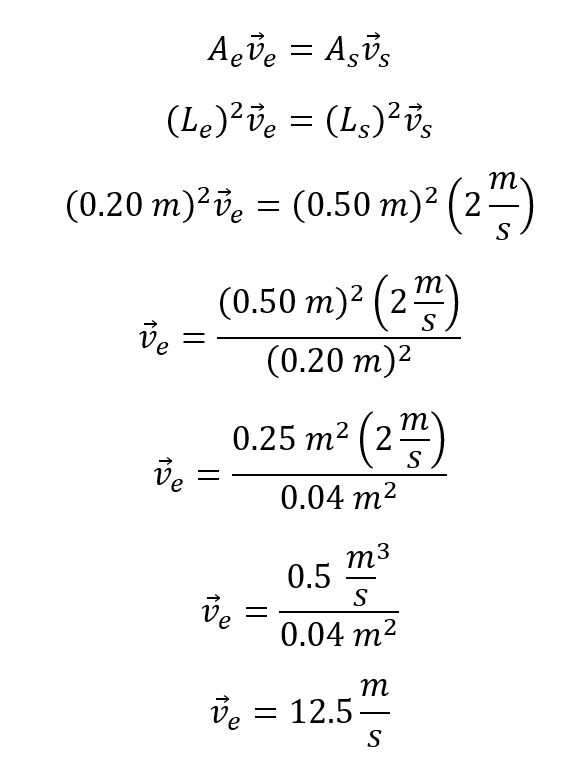
Ejercicio 4. Calcular la velocidad de salida de una tubería por la que fluye un caudal conociendo los datos de entrada.
¿Con qué velocidad saldrá agua de una tubería si la velocidad de entrada es de 8 m/s y las áreas de entrada y de salda son 4 y 1 metros cuadrados respecivamente?
Solución
En este ejercicio se conocen los datos del área tanto a la entrada como a la salida de la tubería por lo que resolverlo será muy sencillo, se utiliza la ecuación de continuidad, se reemplazan los datos de velocidad y áreas conocidas y se despeja la incógnita que para el caso es la velocidad de salida, vamos a hacerlo:
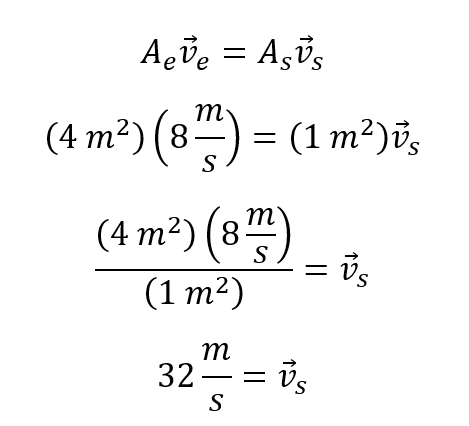



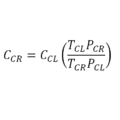

Por qué a la relación del gasto entre el área se le denomina velocidad media?
V=Q/A.
En física, la velocidad es la distancia recorrida por unidad de tiempo. En este contexto, la velocidad media se refiere a la cantidad de algo (Q) que se gasta o se distribuye en relación con el área (A) en un período determinado.