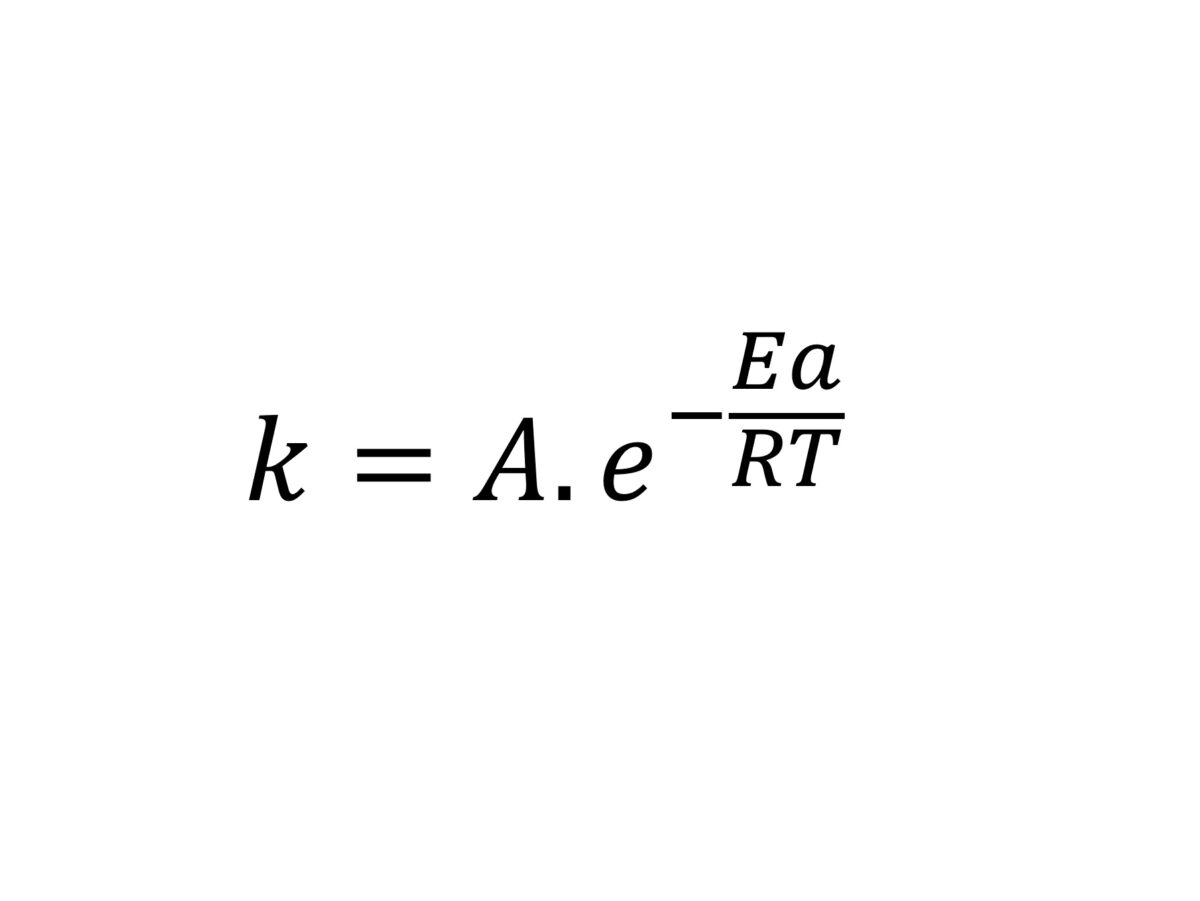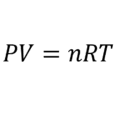La ecuación de Arrhenius es la expresión matemática que relaciona la constante de velocidad con la temperatura en una reacción química. El desarrollo que realizó Svante Arrhenius de esta ecuación se basa en el trabajo del químico neerlandés Van’t Hoff adicionando datos empirícos, es decir diferentes experimentos hasta encontrar la correlación que mejor se ajusta.
Tabla de contenidos
¿Qué dice la ecuación de Arrhenius?
De forma sencilla, la ecuación de Arrhenius muestra la dependencia de la constante de velocidad k, de las reacciones químicas a una temperatura T y la energía de activación Ea de acuerdo con la expresión:
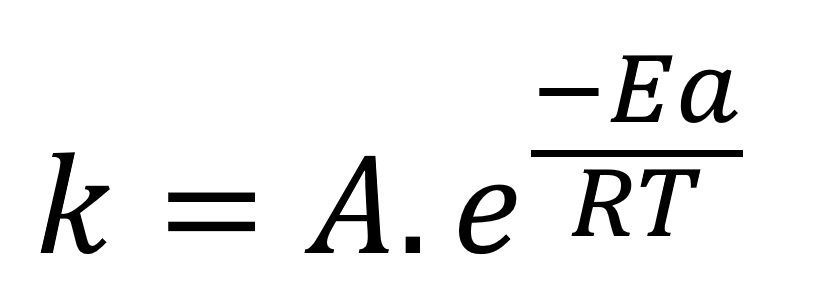
Donde,
k: es la constante cinética (depende de la temperatura)
A: es el factor preexponencial o factor de frecuencia.
Ea: energía de activación en J/mol
R: constante universal de los gases ideales (8,314 J/mol-k)
T: temperatura en Kelvin
¿Cómo afecta la temperatura a la ecuación de Arrhenius?
La temperatura es escencial para comprender la ecuación de Arrhenius, a medida que esta se incrementa la constante cinética de la reacción también aumenta de forma exponencial, esto se explica debido a que cuando la temperatura aumenta, la energía cinética de las moleculas aumenta y esto hace que sea más propensa a superar la energía de activación lo que resulta en una aceleración de la reacción.
Teniendo esto en cuenta la temperatura afecta a una reacción en básicamente cuatro aspectos que son:
- Velocidad de reacción: a mayor temperatura, mayor velocidad de reacción
- Aceleración de reacciones endotérmicas: estas reacciones necesitan de energía para que puedan suceder, un aumento de la temperatura conlleva una absorción mayor de energía por lo que la reacción se hace más viable.
- Influencia en la selectividad: las rutas de reacción pueden dar lugar a reacciones deseadas que no suceden a temperaturas bajas por lo que se obtiene un producto deseado en la reacción química y no otros posibles subproductos.
- Vida media: la vida media de un reactivo se ve afectada por la reacción ya que puede acelerar el cambio a producto.
¿Cuál es el orden de reacción?
En una reacción convencional el orden de reacción se refiere a cómo la velocidad depende de la concentración de los reactivos, normalmente es un número entero, 1, 2, 3, etc.
Sin embargo de acuerdo con la ecuación de Arrhenius el orden de reacción puede variar en función de la temperatura, por lo que se puede tener una reacción donde a temperatura ambiente la cantidad de producto que se forme es mínimo pero al empezar a calentar la cantidad de producto aumenta, es decir el orden de reacción fue modificado.
¿Cuál es la constante de Arrhenius?
Dependiendo de cada reacción química y las condiciones en las que estas se llevan a cabo puede variar el valor de la constante de Arrhenius, aquí te dejamos algunas que pueden ser de gran utilidad:
| Nombre de la reacción | Estequiometría de la reacción | Constante A | Energía de activación |
| Descomposición del peróxido de hidrógeno | 2H2O2->2H2O+O2 | 5,7 x 10^11 s^-1 | 75,6 kJ/mol |
| Formación de amoníaco (síntesis de Haber) | N2 + 3H2 -> 2NH3 | 1,6 x 10^9 L^2/mol^2-s | 175,9 kJ/mol |
| Descomposición térmica del hidrogenoioduro | 2HI-> H2+I2 | 2,4 x 10^6 s^-1 | 186,6 kJ/mol |
| Degradación del ácido acético | CH3COOH->CH4+CO2 | 1,1 x 10^16 s^-1 | 181.6 kJ/mol |
| Oxidación de benceno a fenol | C6H6+O2->C6H5OH | 1,3×10^16 L/mol-s | 126,7 kJ/mol |
| Degradación del perfluorooctanoico (PFOA) | C7F15COOH->8HF+CO2 | 2,3×10^4 s^-1 | 143,5 kJ/mol |
| Descomposición del peróxido de sodio | 2Na2O2->2Na2O+O2 | 2,5×10^9 s^-1 | 165,2 kJ/mol |
| Formación de óxido nítrico | N2+O2->2NO | 6,2 x 10^15 cm^3/mol-s | 166,7 kj/mol |
| Descomposición del ácido nitroso | 2HNO2->H2O+2NO | 1,2 x 10^10 s^-1 | 1447,2 kJ/mol |
Gráfica ecuación de Arrhenius
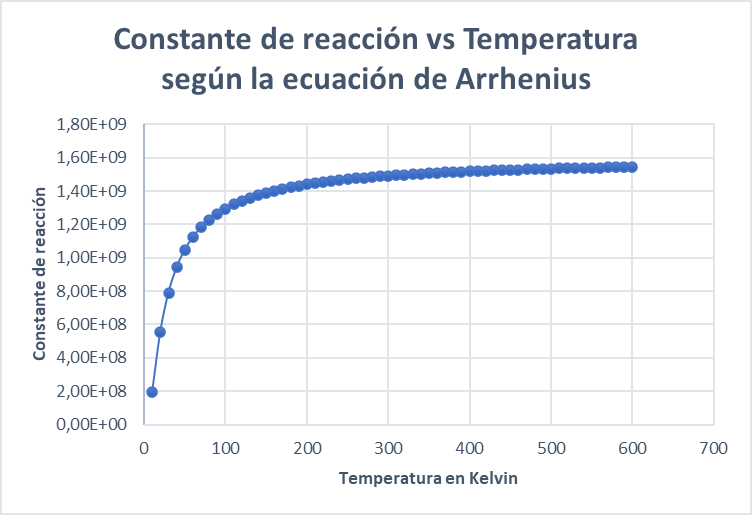
El comportamiento que tiene la gráfica refleja la naturaleza de la ecuación de Arrhenius y de la constante de reacción de acuerdo con el incremento de la temperatura.
Al ser una función exponencial, a temperaturas bajas la constante es baja, pero, a medida que se va incrementando la temperatura la constante empieza a tener un mayor valor, sin embargo llega un punto donde por más que crezca el valor de la temperatura la constante no sufre cambios significativos.
Para estudiar de forma más detallada este comportamiento tomaremos como ejemplo la reacción de formación de amoníaco (síntesis de Haber) donde:
A= 1,6 x 10^9 L^2/mol^2-s
Ea= 175,9 kJ/mol
R= 8,314 J/mol-K
Se obtienen los siguientes resultados:
| Temperatura en Kelvin | Constante de reacción k |
| 10 | 1,93E+08 |
| 20 | 5,56E+08 |
| 30 | 7,90E+08 |
| 40 | 9,43E+08 |
| 50 | 1,05E+09 |
| 60 | 1,12E+09 |
| 70 | 1,18E+09 |
| 80 | 1,23E+09 |
| 90 | 1,26E+09 |
| 100 | 1,29E+09 |
Si graficamos en en el eje y la constante de reacción y en el eje x la temperatura obtenemos:
Ecuación linealizada
En muchos casos cuando se quiere estudiar la ecuación de Arrhenius de forma experimental resulta más fácil graficar los datos mediante un modelo linealizado, para poder hacer esto debemos trabajar la ecuación como:
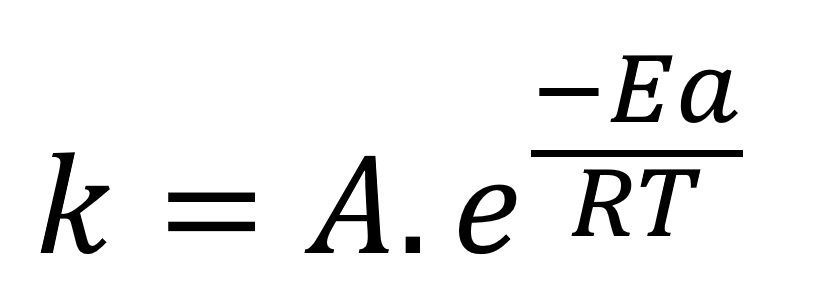
Aplicando logaritmo natural en ambas partes de la ecuación obtenemos:
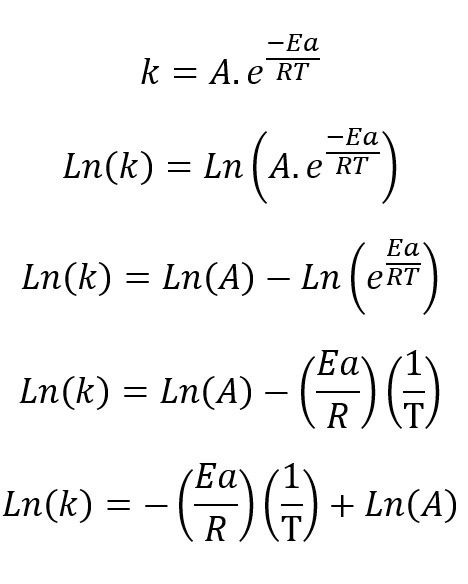
Si observamos detenidamente esta ecuación tiene la estructura de una ecuación de primer grado
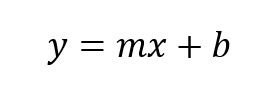
Es decir que:
y=Ln(k)
m=-Ea/R
x= 1/T
b= Ln(A)
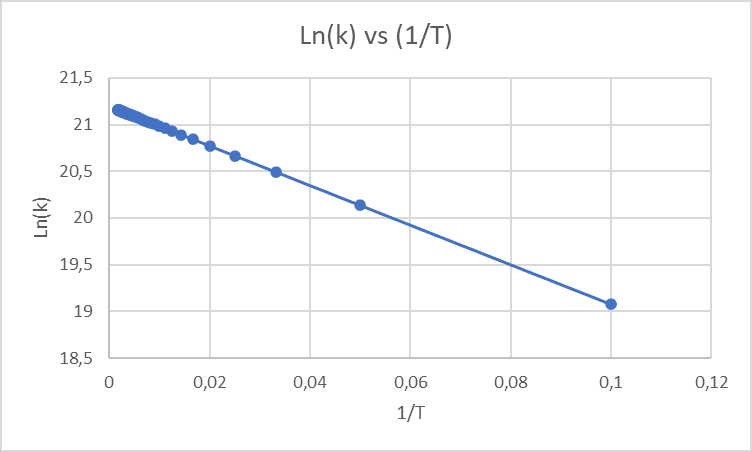
Al graficar la ecuación de Arrhenius linealizada se va a tener en el eje y los valores de Ln(k) en el eje x los valores de 1/T, la pendiente es -Ea/R y el punto de corte del eje y será Ln(A) siguiendo con el mismo ejemplo de la reacción de formación de amoníaco (síntesis de Haber) donde:
A= 1,6 x 10^9 L^2/mol^2-s
Ea= 175,9 kJ/mol
R= 8,314 J/mol-K
La gráfica sería:
Ecuación de Arrhenius para dos temperaturas
Cuando se quiere hacer la comparativa de una reacción química a diferentes temperaturas resulta bastante útil el hecho de tener la ecuación ya linealizada debido a que a partir de los logaritmos naturales hacer el análisis resulta más fácil.
Para estudirar la constante de reacción a dos temperaturas diferentes simplemente modificamos la ecuación linealizada por:
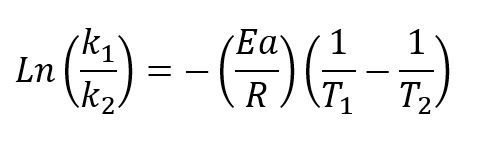
Cabe resaltar que en ambos casos la constante A es la misma por eso no se tiene en cuenta cuando se comparan las constantes de reacción a dos temperaturas diferentes.
Limitaciones
Las reacciones que normalmente se estudian mediante la ecuación de Arrhenius se dan en soluciones acuosas por lo que una limitación importante es la aplicación en otros estados como lo son los sólidos o los gases.
Además al ser una ecuación donde los valores de la constante A se obtienen mediante métodos experimentales estos limitan la información que se puede obtener y también pueden depender de las condiciones en las que se realiza dicho experimento.
Ejemplos resueltos
Se está estudiando la influencia de la temperatura en la constante cinética de una reacción en función de la temperatura y se obtiene:
| Temperatura | k |
| 10 | 3,31E+02 |
| 20 | 1,99E+06 |
| 30 | 3,62E+07 |
| 40 | 1,55E+08 |
| 50 | 3,69E+08 |
| 60 | 6,60E+08 |
| 70 | 9,98E+08 |
| 80 | 1,36E+09 |
| 90 | 1,73E+09 |
| 100 | 2,10E+09 |
Teniendo en cuenta esos datos calcule la energía de activación de la reacción.
Solución
Lo primero que se debe hacer cuando se pide la energía de activación es tomar la gráfica linealizada.
Para poder hacerlo recordemos que debemos tomar los valores de 1/T y de Ln(k) entonces la tabla quedaría transformada a:
| 1/T | Ln(k) |
| 0,1 | 5,80 |
| 0,2 | 14,5 |
| 0,3 | 17,40 |
| 0,4 | 18,85 |
| 0,5 | 19,72 |
| 0,6 | 20,30 |
| 0,7 | 21,03 |
| 0,8 | 21,27 |
| 0,9 | 21,46 |
| 0,01 | 21,62 |
Con estos valores la gráfica sería:
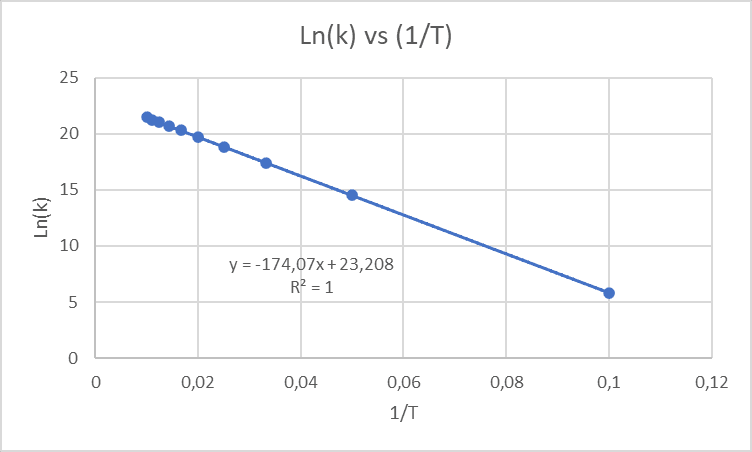
En este caso la pendiente equivale a -Ea/R es decir a -174,07.
Despejando el valor de Ea se tiene entonces que la energía de activación de la reacción es de 1447,2 kJ/mol.
Ejemplo 2:
La reacción de descomposición del peróxido de hidrógeno Ea=75,6 kJ/mol tiene una constante de 5,01E+11 s^-1 a una temperatura de 70 Kelvin
Teniendo en cuenta la información ¿cuál será la constante a 200 K?
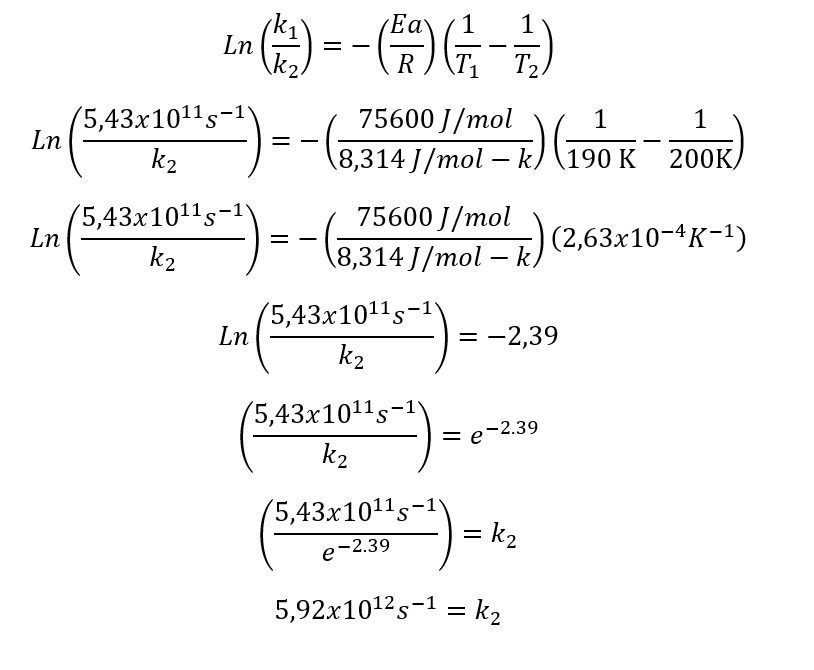
¿Cómo referenciarnos?
Munévar, R. (S.F) Ecuación de Arrhenius. ecuacionde.com. Recuperado el día (fecha en la que nos consultas) de https://ecuacionde.com/arrhenius
Recuerda que si tienes dudas frente a este tema puedes dejar tu pregunta en los comentarios o en nuestra página de contacto
Gracias por visitar nuestra página web.