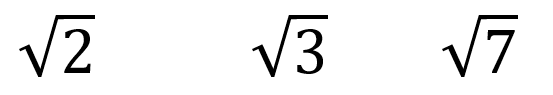Por definición los números reales son todos aquellos que se puede representar como un punto en la recta numérica real, allí están incluidos los números naturales, los números enteros, los números racionales y los números irracionales.
En otras palabras es cualquier número que se encuentre en el intervalo desde menos infinito hasta más infinito (-∞, ∞)
Tabla de contenidos
¿Cómo se representan los números reales?
Los números reales se representan a través de la letra R.
Representación de los números reales en la recta real
Si se utiliza la recta real los números reales abarcan todos los puntos desde menos infinito hasta más infinito, por lo que cualquier punto de la recta es un número real.

Dominio de los números reales
Otra forma común de representar los números reales es a través del dominio, nuevamente el número real es cualquier número que se encuentre en el intervalo desde menos infinito hasta más infinito (-∞, ∞)
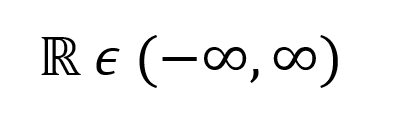
¿Qué características tienen los números reales?
Los números reales tienen cuatro características principales que son:
Infinitud
Los números reales son infinitos, desde un punto de vista más técnico se puede decir que la cantidad de elementos del conjunto de números reales es infinita, no tiene final y son infinitos tanto del lado positivo como del lado negativo.
Orden
Aunque la cantidad de números reales es infinita todos tienen un orden, se puede conocer la posición de cada número real en la recta, entre más a la derecha se encuentre el número este será mayor, por lo tanto, entre más a la izquierda se encuentre un número este será menor.
Por ejemplo si tomamos dos números reales cualquiera, supongamos a y b existen dos posibilidades:
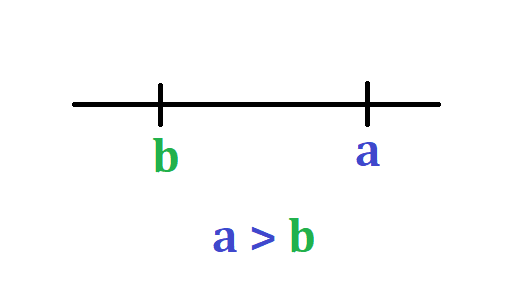
- a > b : la primera posibilidad es que a sea mayor que b es decir que en la recta el número a se encuentra más a la derecha que el número b. Gráficamente esto se representa como:
- b > a : la segunda posibilidad es que b sea mayor que a es decir que en la recta el número b se encuentra más a la derecha que el número a. Gráficamente esto se representa como:
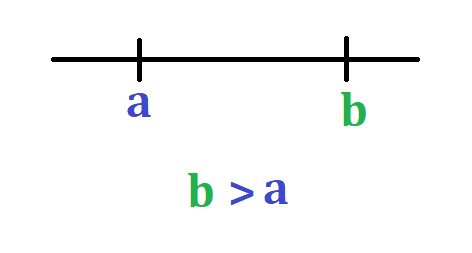
De este modo podemos establecer el orden de todos y cada uno de los números reales.
Integralidad
El conjunto de los números reales es integral, esto significa que no hay espacios vacíos, por ejemplo entre el número 1 y el número 2 hay también una cantidad infinita de números, por ejemplo el 1,1 el 1,2 el 1,3 y así sucesivamente, pero entre el número 1,1 y el número 1,2 también hay una cantidad infinita de elementos que son por ejemplo 1,11 – 1,12 -1,13…
Matemáticamente se establece esta característica como que cada conjunto tiene un límite superior y tiene un límite inferior más pequeño.
Expansión decimal
Los números reales se pueden expresar como decimales y su expansión (o longitud) puede ser finita o infinita. Por ejemplo los números irracionales tienen cifras decimales infinitas e irrepetibles, por ejemplo la raíz cuadrada de dos es aproximadamente 1,4142135623… hay otros números que tienen expansiones finitas, es decir que tienen un final, por ejemplo el 1/2 que equivale a 0,5 y hay otros números que tienen expansiones infinitas pero que son periódicas, es decir que se repiten por ejemplo 1/3 que es 0,3333333…
Todos los números reales tienen una aplicación bien sea en cantidades continuas como longitud o tiempo así como en cantidades no continuas para hacer cálculos matemáticos.
Axiomas de los números reales
Los números reales tienen 15 axiomas que en alguna bibliografía también se conocen como propiedades que son:
Cerradura en la suma
Si un número cualquiera pertenece a los números reales y se suma con otro número que también pertenezca a los números reales el resultado de esa adición también pertenecerá a los números reales sin importar cuáles dos números se hayan tomado inicialmente.
Matemáticamente se representa: si x,y ∈ ℝ entonces x+y ∈ ℝ.
Ejemplo: el número 5 pertenece a los reales, el número -8 pertenece a los reales entonces 5 + (-8) = -3 esto hace que por definición -3 también pertenezca a los números reales.
Conmutatividad en la suma
Si dos números pertenecen a los números reales entonces el resultado de sumar el primero más el segundo es exactamente igual que sumar el segundo más el primero.
Matemáticamente se representa: si x,y ∈ ℝ, entonces x+y=y+x
Ejemplo: El número 14 pertenece a los reales, el número 6 pertenece también a los reales, entonces: 14+6 = 20 = 6+14
Asociatividad en la suma
Si se tienen tres números reales la suma de los dos primero más el tercero es exactamente igual que si se sumaran los dos últimos más el primero.
Matemáticamente se representa: si x,y,z ∈ ℝ, entonces (x+y)+z=x+(y+z)
Ejemplo: Se tienen los números -4, -10 y 6 entonces:
(-4+(-10))+6
-14+6
-8
Por otro lado
-4+(-10+6)
-4+(-4)
-8
Entonces (-4+(-10))+6 = -8 =-4+(-10+6)
Neutro aditivo
Existe un elemento que al ser sumado con cualquier otro número real se obtiene como resultado el mismo número real. Ese elemento es el número cero.
Matemáticamente se representa: Existe 0 ∈ ℝ, tal que x+0=x para todo x ∈ ℝ
Ejemplo: Se tiene un número real π (pi) entonces π + 0 = π
Inverso aditivo
Para cualquier número real existe un inverso aditivo que al ser sumado con el número el resultado es cero.
Matemáticamente se representa:
Para cada x ∈ ℝ, existe -x ∈ ℝ tal que x+(-x) =0
Ejemplo: Se tiene un número real 2/3 por lo que existe -2/3 y:
2/3 + (-2/3) = 0
Cerradura de la multiplicación
Si un número cualquiera pertenece a los números reales y se multiplica con otro número que también pertenezca a los números reales el resultado de esa multiplicación también pertenecerá a los números reales sin importar cuáles dos números se hayan tomado inicialmente.
Matemáticamente se representa: si x,y ∈ ℝ entonces xy ∈ ℝ.
Ejemplo: el número 5 pertenece a los reales, el número -8 pertenece a los reales entonces 5 x (-8) = -40 esto hace que por definición -40 también pertenezca a los números reales.
Conmutatividad en la multiplicación
Si dos números pertenecen a los números reales entonces el resultado de multiplicar el primero por el segundo es exactamente igual que multiplicar el segundo por el primero.
Matemáticamente se representa: si x,y ∈ ℝ, entonces xy=yx
Ejemplo: El número 14 pertenece a los reales, el número 6 pertenece también a los reales, entonces: 14×6 = 84 = 6×14
Asociatividad en la multiplicación
Si se tienen tres números reales la multiplicación de los dos primero por el tercero es exactamente igual que si se multiplicaran los dos últimos por el primero.
Matemáticamente se representa: si x,y,z ∈ ℝ, entonces (xy)z=x(yz)
Ejemplo: Se tienen los números -4, -10 y 6 entonces:
(-4x(-10))x6
40×6
240
Por otro lado
-4x(-10×6)
-4x(-60)
240
Entonces (-4x(-10))x6 = 240 =-4x(-10×6)
Neutro multiplicativo
Existe un elemento que al ser multiplicado con cualquier otro número real se obtiene como resultado el mismo número real. Ese elemento es el número uno.
Matemáticamente se representa: Existe 1 ∈ ℝ , (1≠0) tal que x(1)=(1)x=x para todo x ∈ ℝ
Ejemplo: Se tiene un número real π (pi) entonces π x 1 = π
Inverso multiplicativo
Para cualquier número real existe un inverso multiplicativo que al ser multiplicado con el número real el resultado es uno.
Matemáticamente se representa:
Para cada x≠0 ∈ ℝ, existe x-1 ∈ ℝ tal que x-1x = 1
Ejemplo: Se tiene un número real 2/3 por lo que existe 3/2 tal que:
2/3 x (3/2) = 1
Distributividad de la multiplicación en la suma
Si se tienen tres números, dos de ellos se están sumando y se quieren multiplicar por el tercero, el resultado es equivalente a la multiplicación del primero con el tercero más la multiplicación del segundo con el tercero.
Matemáticamente se representa:
si x,y,z ∈ ℝ, entonces (x+y)z=xz+yz
Ejemplo: Se tienen 3 números 5,6,7 entonces:
(5+6) x 7
11 x 7
77
(5 x 7) + (6 x 7)
35+42
77
(5+6) x 7 = 77 = (5 x 7) + (6 x 7)
Tricotomía
Si se toman dos números reales al azar existen únicamente tres posibilidades:
- Que el primer número sea menor que el segundo
- Que el primer número sea mayor que el segundo
- Que ambos números sean iguales.
Matemáticamente se representa: si x,y ∈ ℝ, entonces solo se cumple una de estas:
- x<y
- x>y
- x=y
Transitividad
Si se tienen tres números tales que el primero es mayor que el segundo y el segundo es mayor que el tercero entonces el primero también es mayor que el tercero.
Matemáticamente se representa: si x,y,z ∈ ℝ, x>y ; y>z entonces x>z
Ejemplo: se tienen tres números reales 20, 5 y -2
20 > 5
5 > -2
Por lo tanto 20 > -2
Monotonía en la suma
Si un número real es mayor que otro y a ambos se les suma la misma cantidad el resultado de la suma que contiene al número que era mayor seguirá siendo mayor que el resultado de la suma que contiene al número menor.
Matemáticamente se representa: si x,y,z ∈ ℝ, x>y entonces x+z > y+z
Ejemplo: se tienen tres números reales 7, 3 y -1 entonces
7 > 3
7+(-1) > 3+ (-1)
6 > 2
Monotonía en la multiplicación
Si un número real es mayor que otro y a ambos se les multiplica por la misma cantidad el resultado de la multiplicación que contiene al número que era mayor seguirá siendo mayor que el resultado de la multiplicación que contiene al número menor, siempre y cuando se haya multiplicado por un número mayor a cero.
Matemáticamente se representa: si x,y,z ∈ ℝ, x>y 0< z entonces xz > yz
Ejemplo: se tienen tres números reales 10, 5 y 2 entonces
10 > 5
10 x 2 > 5 x 2
20 > 10
Clasificación de los números reales
Los números reales están conformados por cuatro subconjuntos de números que son
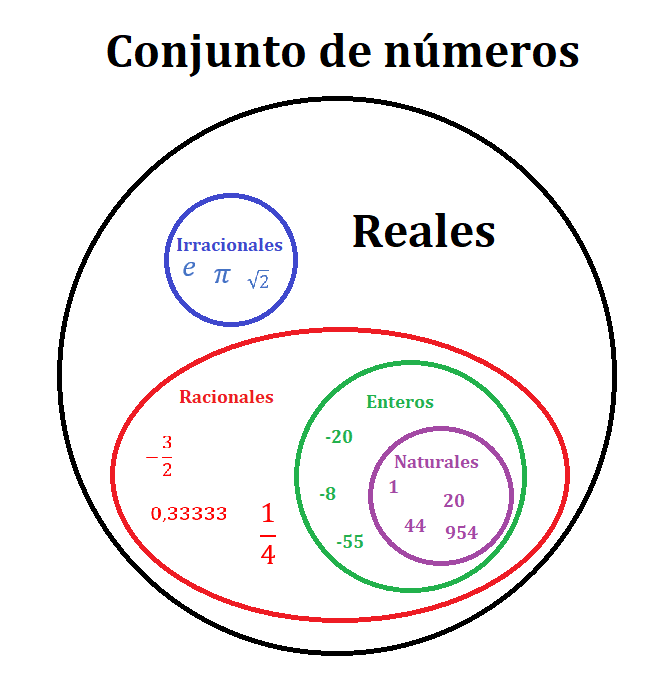
Números naturales
Los números naturales fueron los primeros números que se utilizaron y nacieron de la necesidad de contar. Estos son el 1, 2, 3, 4, 5, 6… hasta el infinito, hay que hacer una claridad y es que el número cero no se encuentra incluido dentro de los números naturales.
Todos los números naturales son la combinación de los diez dígitos 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 no hay letras ni símbolos especiales para escribirlos.
El conjunto compuesto por los números naturales se designa con la letra N.

Ejemplos de números naturales
Los números naturales sirven para contar por ejemplo cuántas personas hay un recinto: «a este recinto asistieron 50 personas» también nos sirve para contar la cantidad de vehículos en un parqueadero: «en este parqueadero hay 4 vehículos» entre otros muchos ejemplos.
Números enteros
El conjunto de números enteros comprende a absolutamente todos los números naturales, a sus números simétricos es decir los que quedan al otro lado de la recta y al cero.
Un número simétrico es aquel que sumado con su correspondiente número natural da como resultado cero. Por ejemplo el simétrico de x es -x, el simétrico de 20 es -20 y así sucesivamente.
Teniendo en cuenta los elementos de este conjunto se puede decir que todos los números naturales también son números enteros, pero no todos los números enteros son números naturales.
Los números enteros se designan con la letra Z y se representan como:
Los números positivos, que son mayores a cero se escriben sin ningún símbolo adicional y los números negativos, que son menores que cero llevan el signo menos antes del valor.
Z={-∞…-4, -3, -2, -1, 0, 1, 2, 3, 4… ∞}
Función de los números enteros
Los números enteros tienen una gran cantidad de aplicaciones en varios campos por ejemplo:
Los números enteros positivos: sirven para mostrar estados de ganancias, temperaturas positivas, distancias hacía la derecha, indicadores de eficiencia.
Los números enteros negativos: sirven para mostrar deudas, pérdidas, temperaturas bajo cero, entre otras.
Ejemplos de números enteros
La temperatura en el polo sur es de -45°C en invierno
Juan le debe 2000 dólares a Pedro, su estado financiero en este momento se encuentra en -2000 dólares.
Números racionales
Los números racionales también conocidos como fraccionarios nacen como una necesidad de dividir cantidades enteras, por ejemplo cuando un padre dejaba un terreno como herencia de 100 hectáreas y esta se debía dividir exactamente entre 3 hijos empezaban a surgir los problemas.
De allí nacen los números racionales que se designan con la letra Q.
Los números racionales son la fracción originada a partir de dos números enteros cuyo denominador es diferente de cero.
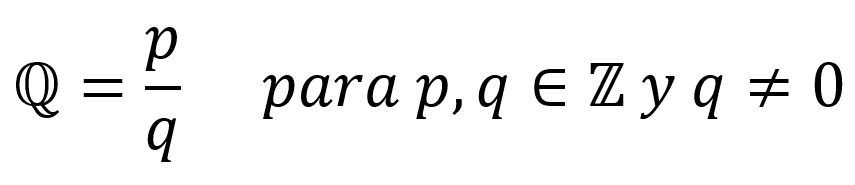
Ejemplos de números racionales
Un pastel se dividió entre 4 personas, cada uno de ellos obtuvo 1/4 del pastel
Un comerciante vendió 3 metros de un paño fino a 5 personas, cada uno de ellos obtuvo 3/5 de metro.
Números irracionales
Los números irracionales son aquellos que no pueden expresarse como la división de enteros en el que el denominador es diferente de cero, este conjunto se representa con la letra I.
Las magnitudes que no pueden expresarse en forma entera o como fracción también se consideran números irracionales, por ejemplo el número Pi π=3,141592 que representa la relación de la circunferencia con el diámetro de un círculo.
Así mismo hay radicales o raíces que no se pueden expresar con números enteros como por ejemplo: