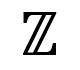Los números naturales surgen de la necesidad que tuvo la humanidad para contar y organizar objetos, aunque inicialmente se utilizaban piedras o palos para este fin, con el tiempo fue necesaria la creación de símbolos que representaran las cantidades y nacieron los números como los conocemos 1, 2, 3, 4, etc…
Tabla de contenidos
¿Qué son los números naturales?
Son un subconjunto de los números reales. De acuerdo con la definición formal son el conjunto de elementos discretos que pertenecen a la recta real y que pueden o no incluir al número cero.
¿Cómo se representan los números naturales?
Existen varias formas de representarlos
Representación con la letra del conjunto
El conjunto de números naturales se representa con la letra N.

Representación con los elementos del conjunto
Si se desea representar como un conjunto sería:
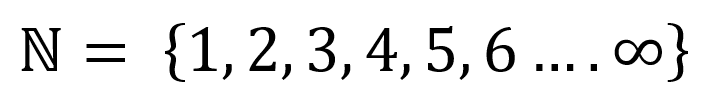
Representación en la recta numérica
En la recta numérica el conjunto de números naturales está representado por:
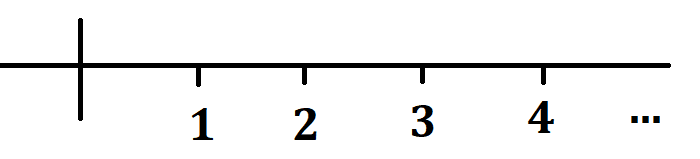
Utilidades de los números naturales
Son utilizados en el día a día sin embargo los usos más importantes son:
Contabilizar los elementos de un conjunto
El conteo de elementos de un conjunto es una actividad que día a día realizamos, por ejemplo:

Hay cuatro huevos en la imagen, el número cuatro denota una cantidad.
Expresar posición u orden de los elementos del conjunto
En muchas ocasiones es necesario establecer la posición de un elemento dentro del conjunto, allí nace otra utilidad, por ejemplo:

Mi hija Mónica quedó en el lugar número 1, en este caso el número natural hace referencia a una posición u orden dentro de un conjunto.
Identificación y diferenciación de los elementos de un conjunto
Este conjunto se utiliza también en la identificación y diferenciación de los elementos de un conjunto. Por ejemplo:

Mark está feliz porque ingresó a trabajar al hospital distrital, su número de trabador es 54 621 y su carnet así lo acredita, en este caso los números naturales sirven para identificar y diferenciar a cada uno de los trabajadores del hospital.
¿Cuáles son las características de los números naturales?
Este conjunto tiene varias características que los hacen particulares:
Orden
Los números naturales tienen un orden creciente, cada uno es el anterior más uno, de este modo podemos conocer la posición de cualquier número.
Por ejemplo sabemos que el número 15 va después del número 14 y a su vez el número 14 va después del 13.
Este orden trae como consecuencia que hayan números naturales mayores o menores que otros.

Por ejemplo podemos decir que 15 es mayor que 14 o sea 15>14 y siguiendo la misma lógica podemos decir que 8 es menor que 10, o sea 8<10.
Conjunto discreto
Los números naturales son un conjunto discreto, es decir entre el número 1 y el número 2 no hay ningún número natural.
Es posible conocer la cantidad de números naturales que hay entre dos elementos.
Infinitud
Los números naturales son infinitos, siempre hay un número mayor, por grande que parezca, por ejemplo si se piensa en el número 9999999948423 parece grande pero después de él está el 9999999948424 y luego el 9999999948425.
No hay un final, siempre hay un número natural más grande que el anterior.
Inicio definido
Aunque los números naturales no tienen un final por sus propiedades de infinitud estos sí tienen un inicio, de este modo el número uno (1) es el primer número natural.
¿Cuáles son los números naturales?
Como te decíamos anteriormente los números naturales son infinitos sin embargo aquí te presentamos los cien primeros
| Nombre | Símbolo | Nombre | Símbolo |
| Uno | 1 | Cincuenta y uno | 51 |
| Dos | 2 | Cincuenta y dos | 52 |
| Tres | 3 | Cincuenta y tres | 53 |
| Cuatro | 4 | Cincuenta y cuatro | 54 |
| Cinco | 5 | Cincuenta y cinco | 55 |
| Seis | 6 | Cincuenta y seis | 56 |
| Siete | 7 | Cincuenta y siete | 57 |
| Ocho | 8 | Cincuenta y ocho | 58 |
| Nueve | 9 | Cincuenta y nueve | 59 |
| Diez | 10 | Sesenta | 60 |
| Once | 11 | Sesenta y uno | 61 |
| Doce | 12 | Sesenta y dos | 62 |
| Trece | 13 | Sesenta y tres | 63 |
| Catorce | 14 | Sesenta y cuatro | 64 |
| Quince | 15 | Sesenta y cinco | 65 |
| Dieciséis | 16 | Sesenta y seis | 66 |
| Diecisiete | 17 | Sesenta y siete | 67 |
| Dieciocho | 18 | Sesenta y ocho | 68 |
| Diecinueve | 19 | Sesenta y nueve | 69 |
| Veinte | 20 | Setenta | 70 |
| Veintiuno | 21 | Setenta y uno | 71 |
| Veintidos | 22 | Setenta y dos | 72 |
| Veintitres | 23 | Setenta y tres | 73 |
| Veinticuatro | 24 | Setenta y cuatro | 74 |
| Veinticinco | 25 | Setenta y cinco | 75 |
| Veintiseis | 26 | Setenta y seis | 76 |
| Veintisiete | 27 | Setenta y siete | 77 |
| Veintiocho | 28 | Setenta y ocho | 78 |
| Veintinueve | 29 | Setenta y nueve | 79 |
| Treinta | 30 | Ochenta | 80 |
| Treinta y uno | 31 | Ochenta y uno | 81 |
| Treinta y dos | 32 | Ochenta y dos | 82 |
| Treinta y tres | 33 | Ochenta y tres | 83 |
| Treinta y cuatro | 34 | Ochenta y cuatro | 84 |
| Treinta y cinco | 35 | Ochenta y cinco | 85 |
| Treinta y seis | 36 | Ochenta y seis | 86 |
| Treinta y siete | 37 | Ochenta y siete | 87 |
| Treinta y ocho | 38 | Ochenta y ocho | 88 |
| Treinta y nueve | 39 | Ochenta y nueve | 89 |
| Cuarenta | 40 | Noventa | 90 |
| Cuarenta y uno | 41 | Noventa y uno | 91 |
| Cuarenta y dos | 42 | Noventa y dos | 92 |
| Cuarenta y tres | 43 | Noventa y tres | 93 |
| Cuarenta y cuatro | 44 | Noventa y cuatro | 94 |
| Cuarenta y cinco | 45 | Noventa y cinco | 95 |
| Cuarenta y seis | 46 | Noventa y seis | 96 |
| Cuarenta y siete | 47 | Noventa y siete | 97 |
| Cuarenta y ocho | 48 | Noventa y ocho | 98 |
| Cuarenta y nueve | 49 | Noventa y nueve | 99 |
| Cincuenta | 50 | Cien | 100 |
Operaciones matemáticas con números naturales
Los números naturales se prestan para realizar las cuatro operaciones básicas de la matemática
Suma de números naturales
Cualquier número natural puede ser sumado con otro número natural y el resultado que se obtenga también va a pertenecer al conjunto de los números naturales.
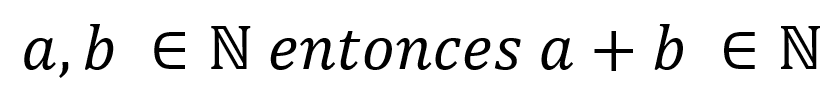
Adicional a esto la suma presenta propiedades conmutativas y asociativas
Propiedad conmutativa
Sumar un número natural a con un número natural b es exactamente igual que sumar b con a.

Por ejemplo 5 + 3 = 8 y a su vez 3 + 5 = 8
Propiedad asociativa
Si se tienen tres números naturales, la suma de los dos primeros más el tercero es equivalente a la suma de los dos últimos más el primero, es decir:
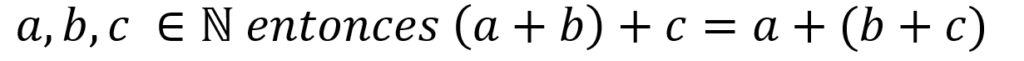
Por ejemplo (4+6)+5 es igual a 10+5=15 si establecemos la propiedad asociativa tenemos que 4+(6+5) = 4+11 = 15
Resta de números naturales
Para que el resultado de una resta pertenezca al conjunto de números naturales al número base se le debe restar un número menor.
De lo contrario se tendrá como resultado un número negativo y recordemos que todos los números naturales son positivos.
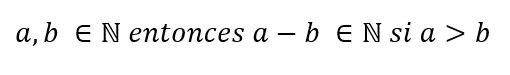
Por ejemplo 10 y 4 pertenecen a los números naturales entonces 10-4 = 6 el resultado 6 también pertenece a los números naturales. Pero si el número que se resta es mayor por ejemplo 10 y 15 entonces 10-15=-5 ese valor negativo no se encuentra dentro de los números naturales.
Multiplicación de números naturales
Cualquier número natural puede ser multiplicado con otro número natural y el resultado que se obtenga también va a pertenecer al conjunto de los números naturales.
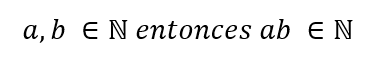
Adicional a esto la multiplicación presenta propiedades conmutativas y asociativas
Propiedad conmutativa
Multiplicar un número natural a con un número natural b es exactamente igual que multiplicar b con a.
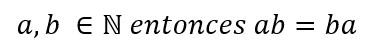
Por ejemplo 5 x 3 = 15 y a su vez 3 x 5 = 15
Propiedad asociativa
Si se tienen tres naturales, la multiplicación de los dos primeros por el tercero es equivalente a la multiplicación de los dos últimos por el primero.
Es decir:
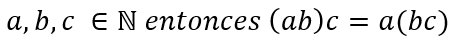
Por ejemplo (4×6)x5 es igual a 24×5=120 si establecemos la propiedad asociativa tenemos que 4x(6×5) = 4×30 = 120
División de naturales
Para que el resultado de una división pertenezca al conjunto de naturales el número base debe ser múltiplo del número divisor.
De lo contrario se tendrá como resultado un número decimal y recordemos que todos los naturales son discretos.
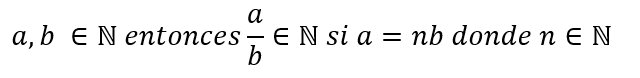
Por ejemplo 12 y 4 pertenecen a los naturales entonces 12/4 = 3 el resultado 3 también pertenece a los naturales.
Si el número que divide fuera otro que no sea múltiplo por ejemplo 12 y 10 entonces 12/10=1,2 ese valor decimal no se encuentra dentro de los naturales.
Axiomas de los naturales
A lo largo de la historia se han presentado varias propuestas para axiomatizar la noción normal de los números naturales, sin embargo las más importantes han sido las propuestas de Peano y la teoría de conjuntos.
Axioma de Peano
- Si se tiene un número natural cualquiera a, entonces el número sucesor (a+1) también es un número natural
- El 1 no es el sucesor de ningún número natural, es decir el conjunto de números naturales inicia en 1.
- Si se escogen dos números aleatoriamente a y b dentro del conjunto de números naturales y ambos tienen el mismo sucesor significa que a=b.
Teoría de conjuntos
Esta definición más elaborada fue simplificada por Von Neumann donde se estableció que:
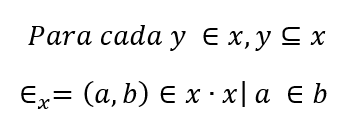
Donde hay un orden total estricto en x y todo subconjunto no vacío de x tiene elementos mínimo y máximo en el orden perteneciente de x.