La notación científica en algunos lugares conocida también como notación exponencial es una forma sencilla de escribir números o muy grandes o muy pequeños basándose en una potencia de 10.
Esto trae muchas ventajas sobre todo en campos como la física o la química donde los valores son frecuentes, adicional a esto la notación científica permite mostrar claramente las cifras significativas y determinar de una forma casi que inmediata las comparaciones de magnitud.
Tabla de contenidos
¿Cuáles son las partes de la notación científica?
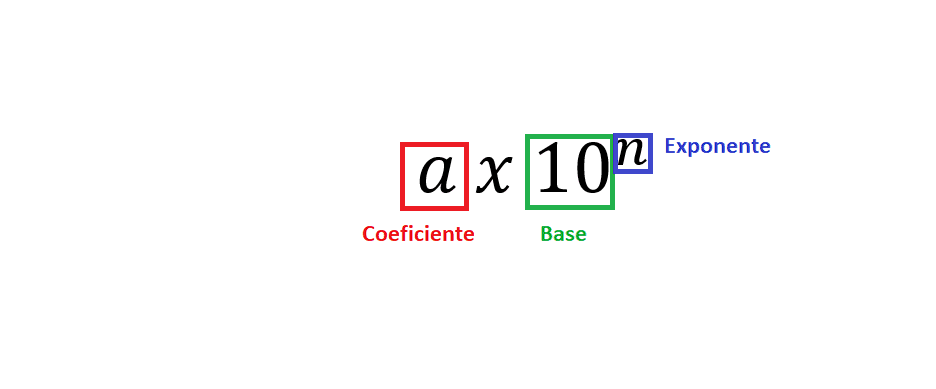
Para poder escribir un número en notación científica es importante reconocer sus partes, estas son:
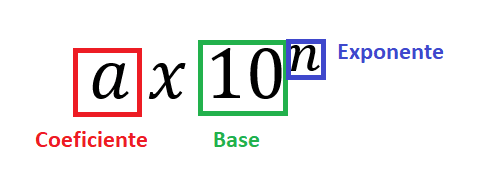
¿Cuál es el formato de la notación científica?
Para que un número sea considerado correctamente escrito en notación científica debe cumplir la forma:
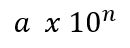
donde:
- Coeficiente (a) debe ser mayor o igual a uno pero menor que diez (1≥a<10)
- Exponente (n) debe ser un número entero
- Base 10 nunca puede ser cambiada
Para comprender mejor estas condiciones vamos a ver algunos ejemplos:
| Número | ¿Es notación científica? | ¿Por qué? |
| 4.25 x 10-2/3 | No | El exponente n debe ser un número entero en este caso -2/3 no es entero |
| 0.25 x 1012 | No | El coeficiente a que en este caso es 0.25 debe ser mayor o igual a uno y menor que diez, 0.25 no es mayor o igual que 1. |
| 2.15 x 8-11 | No | La base 10 nunca puede ser cambiada, en este ejemplo se puso un 8. |
| 1.23 x 10-6 | Si | El exponente n es entero, en este caso es -6. El coeficiente a que en este caso es 1.23 es mayor o igual que 1 y menor que 10. La base 10 no fue cambiada |
¿Cómo pasar de decimal a notación científica?
La clave para pasar números decimales muy grandes o muy pequeños a notación científica es el movimiento de la coma y depende si los números que queremos pasar son muy grandes o muy pequeños.
Números muy grandes
Vamos a utilizar un ejemplo de un número muy grande para pasar a notación científica, 4 562 000 000 000
Lo primero es identificar si tiene decimales, en este caso el número no tiene decimales por lo que ponemos la coma en el último cero así:
4 562 000 000 000,
No hemos movido a ninguna posición por lo que empezamos a añadir la base y el exponente para que vaya tomando la forma de la notación científica, como no se ha hecho ningún movimiento el exponente empieza con cero:
4 562 000 000 000, x 100
Empezamos a correr la coma número por número hacía la izquierda y cada vez que lo hacemos vamos sumando uno al exponente, de esta forma:
- 4 562 000 000 000, x 100
- 4 562 000 000 00,0 x 101
- 4 562 000 000 0,00 x 102
- 4 562 000 000, 000 x 103
- 4 562 000 00,0 000 x 104
- 4 562 000 0,00 000 x 105
- 4 562 000, 000 000 x 106
¿Hasta qué posición debemos hacerlo? recuerda que el coeficiente a es decir lo que está a la izquierda de la coma debe ser menor que 10, entonces continuamos…
- 4 562 00,0 000 000 x 107
- 4 562 0,00 000 000 x 108
- 4 562, 000 000 000 x 109
- 4 56,2 000 000 000 x 1010
- 4 5,62 000 000 000 x 1011
- 4, 562 000 000 000 x 1012
En este punto no podemos correr más la coma porque si lo hacemos tendríamos como coeficiente 0.4562 y recordemos que el coeficiente siempre debe ser mayor que 1. Entonces paramos en:
4, 562 000 000 000 x 1012
Pero la idea de la notación científica es reducir la cantidad de ceros, ¿lo recuerdas? los ceros a la derecha de una coma no son necesarios de ser escritos por lo que en notación científica el número 4 562 000 000 000 queda escrito como:
4, 562 x 1012
Ejemplo #2
Es un procedimiento que con la práctica cada vez irás haciendo más rápido, vamos a ver ahora un ejemplo si el número tuviera decimales. Vamos a pasar a notación científica el número 1 325 600,23 realizamos el mismo procedimiento
- 1 325 600,23
- 1 325 600,23 x 100
- 1 325 60,023 x 101
- 1 325 6,0023 x 102
- 1 325 ,60023 x 103
- 1 32,5 60023 x 104
- 1 3,25 60023 x 105
- 1 ,325 60023 x 106
En este caso el número 1 325 600,23 en notación científica se escribe 1 ,325 60023 x 106
Números muy pequeños
Ahora vamos a utilizar un ejemplo de un número muy pequeño para pasar a notación científica 0, 000 000 000 987
Al igual que en los ejemplos anteriores lo primero es escribir el número con la base y el exponente cero, quedando:
0, 000 000 000 987 x 100
En los números pequeños vamos a empezar a correr la coma hacía la derecha entonces cada posición que la corramos vamos a restarle uno al exponente, así:
- 0 0,00 000 000 987 x 10-1
- 0 00,0 000 000 987 x 10-2
- 0 000, 000 000 987 x 10-3
- 0 000 0,00 000 987 x 10-4
- 0 000 00,0 000 987 x 10-5
- 0 000 000, 000 987 x 10-6
- 0 000 000 0,00 987 x 10-7
- 0 000 000 00,0 987 x 10-8
- 0 000 000 000, 987 x 10-9
Recuerda que el coeficiente debe ser mayor o igual a 1 y menor que 10 por lo que falta correr la coma una posición más
0 000 000 000 9,87 x 10-10
9,87 x 10-10
Los ceros a la izquierda de una coma no tienen valor por lo que podemos decir que 0, 000 000 000 987 escrito en notación científica es 9,87 x 10-10
Si te sigue pareciendo muy difícil te voy a dejar una calculadora que pasa de números decimales a notación científica para que se te facilite el trabajo
Calculadora de decimal a notación científica
¿Cómo pasar de notación científica a decimal?
Al igual que en el caso anterior existe la posibilidad de pasar números o muy grandes o muy pequeños de notación científica a notación decimal.
Números muy grandes
Cuando tenemos un numero con exponente positivo sabemos que es muy grande, para completar el número debemos hacerlo con ceros como se explicará a continuación. Pasar 6,14 x 105 a decimal:
Lo primero es empezar a correr la coma hacía la derecha, cada vez que lo hagamos le vamos a restar un número al exponente, vamos a realizar este procedimiento hasta llegar a exponente cero.
6,14 x 105
61,4 x 104
614, x 103
En este caso no tenemos más números para seguir corriendo la coma por lo que vamos a completar con ceros así:
6140, x 102
61400, x 101
614000, x 100
Una vez se llegue al exponente cero podemos decir entonces que 6,14 x 105 es igual a 614 000
Ejemplo #2 pasar números muy grandes a decimal
Si un número grande llega a tener más dígitos que las posiciones que podemos correr con el exponente no hay ningún problema, por ejemplo:
8,12568463 x 105
Con este número por ejemplo podemos ver que hay 8 dígitos después de la coma pero el exponente solo es 5, eso no es ningún inconveniente, empezamos a hacer el procedimiento de correr la coma a la derecha mientras le restamos un número al exponente hasta llegar a cero.
81,2568463 x 104
812,568463 x 103
8125,68463 x 102
81256,8463 x 101
812568,463 x 100
Eso significa que el número 8,12568463 x 105 escrito en decimal es 812 568,463 (la coma queda ubicada en esa posición).
Números muy pequeños
Cuando un número está escrito en notación científica y el exponente es negativo sabemos de antemano que estamos ante un número muy pequeño, para pasar un número muy pequeño de notación científica a decimal debemos correr la coma hacía la izquierda y completar con ceros a medida que le sumamos uno al exponente como se muestra en el siguiente ejemplo:
7,124 x 10-4
0,7124 x 10-3
0,07124 x 10-2
0,007124 x 10-1
0,0007124 x 100
A través de ese proceso podemos concluir que 7,124 x 10-4 es igual a 0,0007124 sin embargo si te sigue pareciendo muy difícil te voy a dejar una calculadora que pasa de notación científica a números decimales para que se te facilite el trabajo
Calculadora de notación científica a decimal
¿Para qué sirve la notación científica?
La mayoría de fenómenos físicos no se encuentran a la escala humana, por ejemplo si nos hacemos la pregunta ¿Cuántos granos de arena hay en las playas del planeta? debemos empezar a realizar ciertas aproximaciones:
En el mundo hay aproximadamente 300 000 km de playas donde en promedio tienen 50 metros de ancho y 25 metros de profundidad, esto significa que el volumen de arena de playa es aproximadamente:
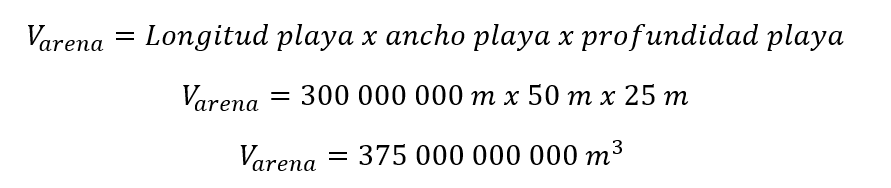
Aproximadamente hay 375 mil millones de metros cúbicos de arena.
De acuerdo con los estudios de Gary Greenberg en un metro cúbico de arena hay 10 mil millones de granos, así que si quisiéramos saber la cantidad total de granos de arena en el mundo debemos multiplicar los metros cúbicos de todas las playas por la cantidad de granos que hay en un metro cúbico.

De acuerdo con las aproximaciones podemos inferir que hay 3 750 000 000 000 000 000 000 granos de arena en el mundo, esta cifra es un número muy extenso por lo que la notación científica la reduce a:
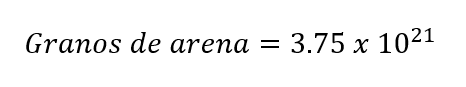
Sin duda alguna es una cifra mucho más amigable ya que no se deben escribir una gran cantidad de ceros.
Ejemplos de números en notación científica
En la naturaleza abundan los números muy grandes o muy pequeños, los casos más emblemáticos son:
Número de Avogadro
Especifica la cantidad de partículas que hay en un mol de sustancia, su valor es de 602 200 000 000 000 000 000 000 es decir seiscientos dos mil doscientos trillones de partículas por mol.
En notación científica encontrarás el número de Avogadro como 6.022 x 1022 partículas por mol.
Carga eléctrica fundamental
La carga que tienen el protón siendo positivo, o el electrón siendo negativo es de 0,000000000000000016 Coulombs.
En notación científica encontrarás la carga eléctrica fundamental equivalente a 1.6 x 10-19 Coulombs.
Masa de un protón
Una de las partes principales del núcleo del átomo y con una carga positiva, el protón tiene una masa de 0,00000000000000000000000166 gramos ¿un poco pequeña no?
En notación científica encontrarás la masa de un protón como 1.66 x 10-24 gramos.
Operaciones matemáticas con notación científica
En ocasiones es necesario operar con números que están escritos en notación científica por eso es importante aprender a hacerlo de forma fácil.
Suma y resta de números escritos en notación científica
Para poder sumar o restar números escritos en notación científica es necesario analizar los exponentes de las bases, dependiendo de como estos sean se determina el proceso de solución.
Suma y resta de números escritos en notación científica con mismo exponente
Realizar la operación entre los coeficientes y si es necesario volver a escribir en notación científica, por ejemplo
6,435 x 104 + 2,15 x 104
Como ambos números tienen el mismo exponente simplemente se suman los coeficientes y se deja la base y el exponente.
(6,435 + 2.15) x 104
8,585 x 104
Este es un caso sencillo, analicemos ahora qué sucede si la cifra de los coeficientes al sumarse resulta un valor superior a 10, por ejemplo:
7,25 x 106 + 4,75 x 106
Al igual que en el ejemplo anterior se suman los coeficientes:
(7,25+4,75) x 106
12 x 106
Pero recordemos que para que sea considerado notación científica el coeficiente no puede ser mayor a 10 y en este caso tenemos 12, por lo que es necesario correr la coma una posición a la izquierda y aumentar en uno el exponente así:
1,2 x 107
Suma y resta de números escritos en notación científica con diferente exponente
En estos casos lo primero que debemos hacer es convertir los números al mismo exponente y luego reescribir en notación científica, por ejemplo:
9,123 x 106 – 1,2 x 105
Lo ideal es escribir el de mayor exponente en términos del menor exponente, para este caso 9,123 x 106 pasaría a ser 91,23 x 105 luego se hace la operación ya que ambos tienen el mismo exponente:
91,23 x 105 – 1,2 x 105
90,03 x 105
Y reescribimos nuevamente en formato correcto de acuerdo con la notación científica.
9,003 x 106
Multiplicación de números escritos en notación científica
El proceso para realizar multiplicación de números escritos en notación científica es un poco más sencillo que el de la suma ya que no importa si los números tienen diferente exponente, simplemente se hace la operación de los coeficientes, se suman las bases y se reescribe de ser necesario en notación científica, por ejemplo:
(5,14 x 103)(4,32×10-1)
Lo primero es que se multiplican los coeficientes
5,14 x 4,32 = 22,2048
Se suman los exponentes de las bases
3 + (-1) = 2
Se escribe el número con el coeficiente y la base resultante
22,2048 x 102
Se hacen los ajustes necesarios para que quede escrito en notación científica
2,22048 x 103
En este caso es correr la coma una posición hacía la izquierda lo que hace que sea necesario sumarle uno al exponente.
División de números escritos en notación científica
El proceso de división de números escritos en notación científica es también muy sencillo, lo primero es dividir los coeficientes, las bases de los exponentes se restan y finalmente se verifica que se cumpla con las condiciones de la notación científica.
Ejemplo # 1 división de números en notación científica
(8,48 x 10-6) /(4,24 x 102)
El primer paso es dividir los coeficientes, en este caso
8,48/4,24 = 2
Luego se restan los exponentes
-6 – 2 = -8
El resultado es:
2 x 10-8
Este número cumple con todas las características de la notación científica por lo que esa es la respuesta.
Ejemplo # 2 división de números en notación científica
(2,1 x 104)/(8,2 x 10-6)
El primer paso es dividir los coeficientes
(2,1 / 8,2) = 0,256097
El segundo paso es restar los exponentes:
4 – (-6) = 4+6 = 10
Se escribe el resultado
0,256097 x 1010
En este caso el coeficiente es menor a 1 y sabemos que no cumple con los criterios de la notación científica por lo que corremos la coma una posición a la derecha y le restamos uno al exponente, la respuesta correcta sería:
2,56097 x 109