El movimiento parabólico, tiro parabólico o tiro oblicuo es el desplazamiento que realiza cualquier objeto cuando la trayectoria describe una parábola.
Es ampliamente utilizado en física y ramas de la ingeniería ya que este movimiento describe la trayectoria ideal de un proyectil

Tabla de contenidos
¿Qué condiciones tiene el movimiento parabólico?
Cuando se están haciendo estudios de movimientos parabólicos inicialmente se tienen que tener en cuenta ciertas restricciones que son:
- El cuerpo que se mueve lo hace a través de un medio que no tiene resistencia, es decir el aire no afecta el movimiento del cuerpo. Nota: a medida que se avanza en el estudio de la física del movimiento se tendrán en cuenta los efectos del aire sobre el cuerpo y la geometría del mismo pero inicialmente se desprecian.
- El cuerpo está sometido a un campo gravitatorio uniforme, es decir a lo largo de su trayectoria la gravedad es constante.
- El cuerpo se mueve en dos direcciones, se desprecian los posibles cambios en una tercera dimensión.
- Se desprecian efectos de largas distancias como la curvatura del planeta Tierra.
¿Qué características tiene el tiro parabólico?
- El movimiento parabólico puede ser analizado como la composición de dos movimientos rectilíneos: un movimiento rectilíneo uniforme horizontal y un movimiento rectilíneo uniformemente acelerado vertical.
- Si se conoce la velocidad inicial de salida, el ángulo de inclinación inicial y la diferencia de alturas entre la salida y la llegada del cuerpo se conocerá toda la trayectoria.
- Los ángulos de salida y llegada son iguales si la altura de salida y llegada también son iguales.
- La distancia máxima cubierta, o de alcance se logra con un ángulo de salida de 45°
- El factor más importante sobre la distancia recorrida es la velocidad de salida.
- El análisis del movimiento global se puede hacer separando el movimiento vertical y el movimiento horizontal
- La componente horizontal se mantiene constante.
Ecuaciones del movimiento parabólico
El movimiento parabólico tiene varias ecuaciones que describen el comportamiento del cuerpo a lo largo de su movimiento, se separan principalmente en tres grupos, las que describen la posición, las que describen la velocidad y las que describen el tiempo:
Ecuaciones de velocidad
Debido a que el movimiento parabolico tiene movimiento tanto en el eje vertical como en el eje horizontal es importante definir los componentes de la velocidad en cada uno de los ejes, para ello se hace una descomposición así:
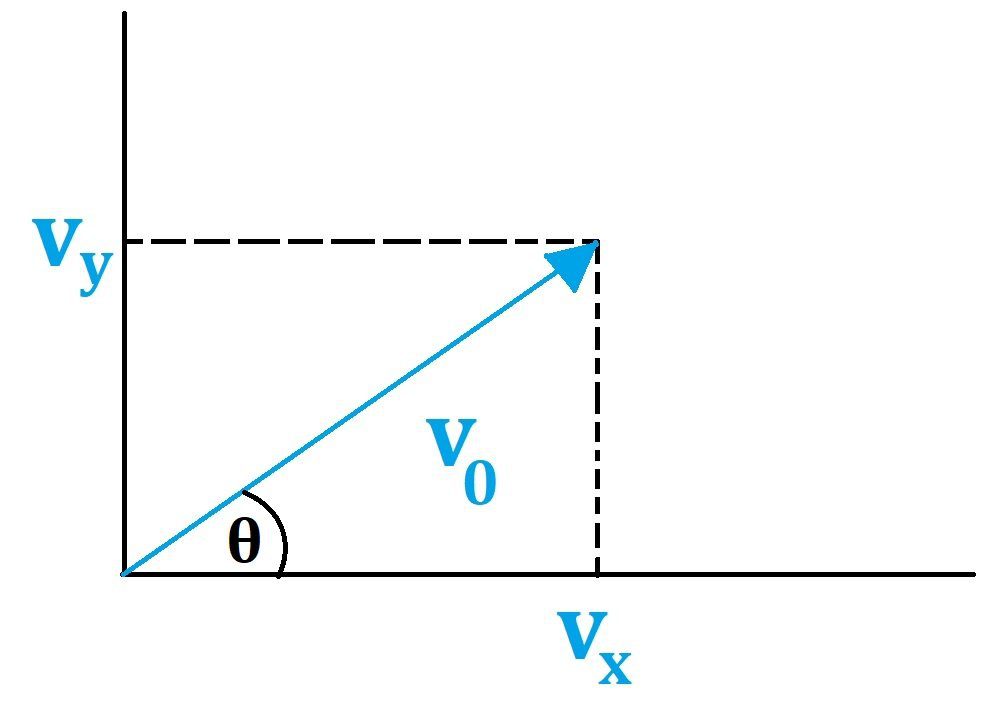
Donde,
vo: es el valor de la velocidad inicial
vx: es el valor de la velocidad en el componente x
vy: es el valor de la velocidad en el componente y
θ: es el valor del ángulo con el que es lanzado el cuerpo
Con base en esto y conociendo el valor de la velocidad inicial con la que se lanza el cuerpo se tiene entonces que:
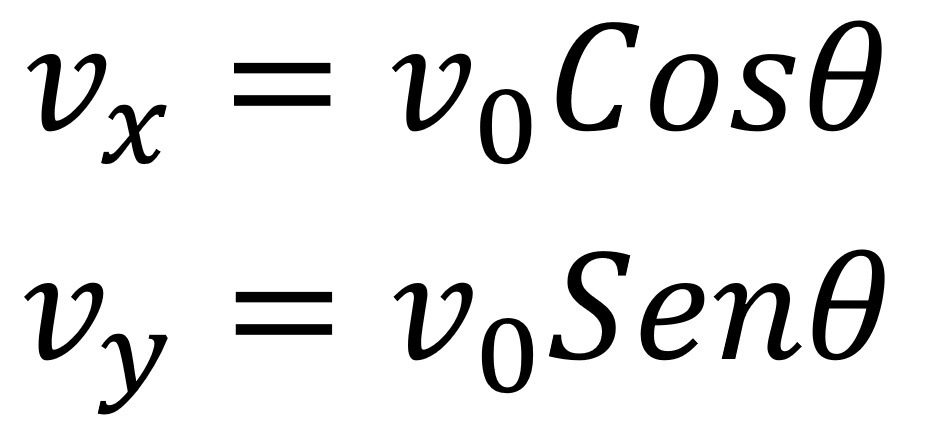
Sin embargo, como en el eje y la gravedad es una aceleración afecta la velocidad, esto no sucede en el eje x, por lo que para el eje vertical se debe tener en consideración la variación en la velocidad por la afectación de la aceleración quedando la ecuaciones así:
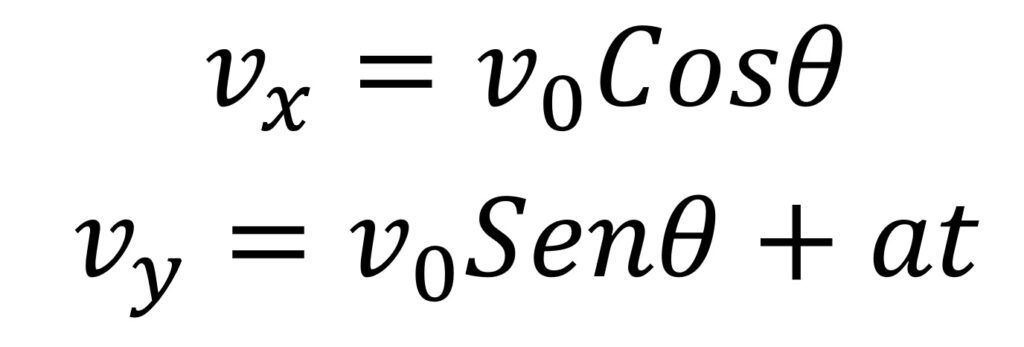
Ecuaciones de posición
Cuando se habla de ecuaciones de posición en el movimiento parabólico lo que se busca es detallar especificamente la ubicación del objeto en un momento determinado bajo un sistema de coordenadas (x,y) donde x representa el eje horizontal y y el plano vertical.
Dentro de las ecuaciones de posición podemos encontrar:
Ecuaciones de posición en el eje x
Empezaremos a describir las ecuaciones del eje x debido a que el movimiento horizontal del cuerpo se puede describir como rectilineo uniforme MRU, en el eje y el movimiento es rectilineo uniforme acelerado MRUA por lo que tiene un poco más de complejidad.
Movimiento en el eje x

Para conocer la ubicación del cuerpo en el eje x se requiere conocer:
x0: es la posición inicial en el eje x, normalmente se expresa en metros.
vx: es la velocidad en el eje x, recuerda que no necesariamente es la velocidad con la que es lanzado el cuerpo sino el valor que tiene en el componente x, más adelante se explicará cómo se calcula. Normalmente se expresa en metros sobre segundo.
t: es el tiempo que ha transcurrido desde que el cuerpo empieza a moverse hasta el instante en el que se quiere conocer su posición, normalmente se expresa en segundos.
Recordando que la velocidad en el componente x depende con el angulo que es lanzado el cuerpo se tiene entonces que:
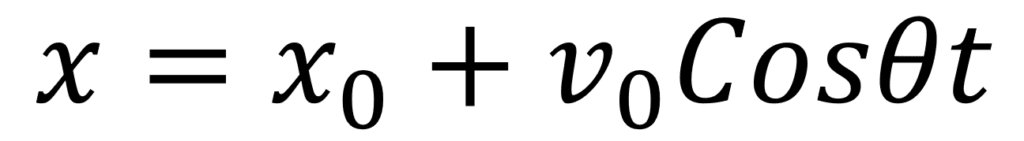
Alcance horizontal máximo
El alcance horizontal máximo es la distancia que recorre el objeto desde el punto de lanzamiento hasta el punto donde toca el suelo. La ecuación que describe este movimiento es:
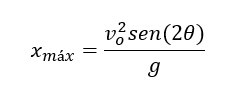
Ecuaciones de posición en el eje Y
Como se mencionaba anteriormente, en el eje y el movimiento es rectilineo uniforme acelerado MRUA, es decir que se ve afectado por una aceleración que se conoce comunmente como gravedad.
Al analizar detalladamente el lanzamiento parabólico se puede evidenciar que tiene dos fases, una de ascenso y una de descenso, la fase de ascenso se puede considerar un lanzamiento vertical, mientras que la fase de descenso se puede considerar una caída libre, por lo tanto las ecuaciones son:
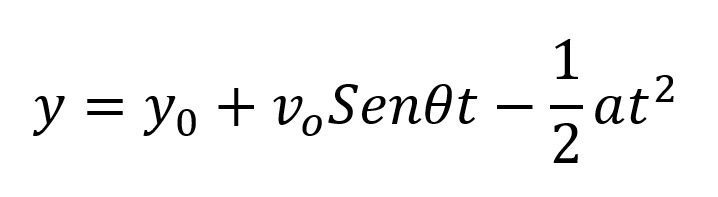
Para las ecuaciones del eje y la aceleración que se utiliza es la gravedad.
Altura máxima
Hay una ecuación que es de especial interés en el movimiento parábolico y es la altura máxima que puede alcanzar el proyectil, esto se puede calcular mediante la ecuación
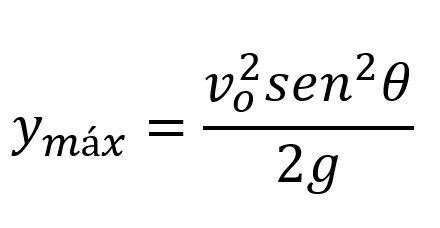
Ejemplo resuelto
Un balón es pateado desde el suelo con un ángulo de 30 grados respecto a la horizontal. La velocidad inicial del balón es de 20 m/s. Calcula la distancia horizontal recorrida, la altura máxima alcanzada y la altura cuando han transcurrido 1,5 segundos.

De acuerdo con las variables que nos piden responder vamos a iniciar con la distancia horizontal recorrida, para ello utilizamos la ecuación:
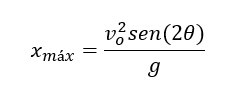
Reemplazando los valores y solucionando tenemos:
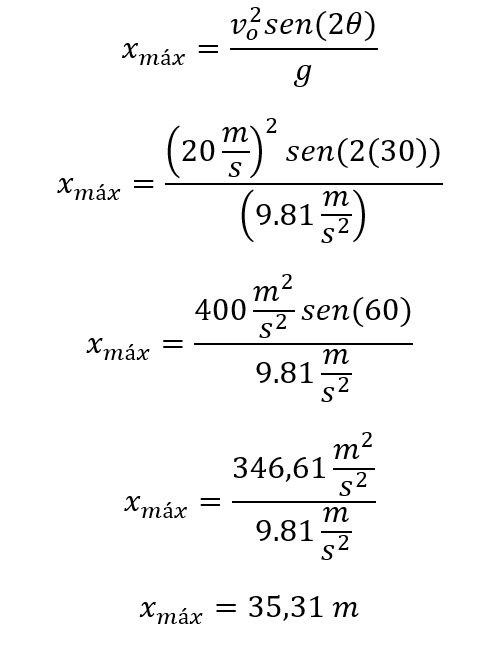
La distancia horizontal que alcanza el balón es de 35,31 metros. Ahora procedemos a calcular la altura máxima con la ecuación:
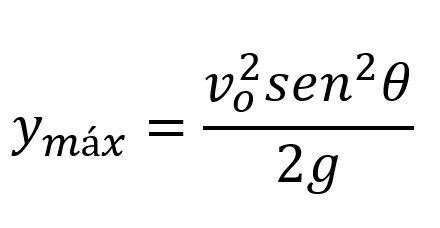
Reemplazando los valores tenemos que:
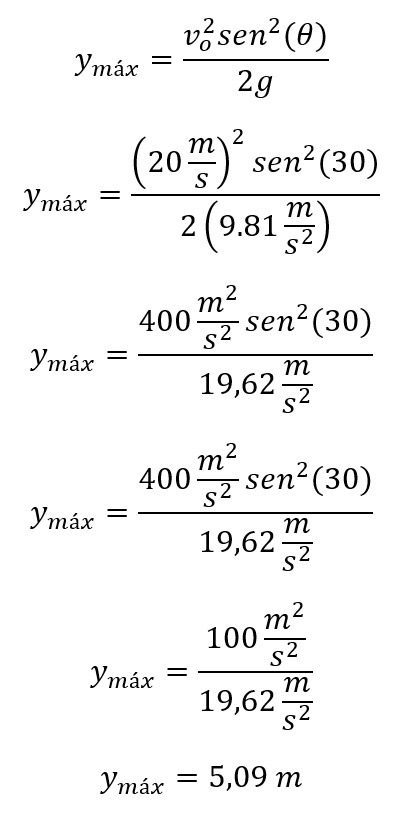
La altura máxima que alcanza el balón es de 5,09 metros. Ahora procedemos a calcular la altura cuando han transcurrido 1,5 segundos con la ecuación:
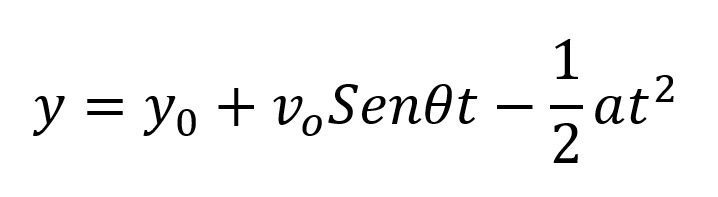
Reemplazando valores tenemos que:
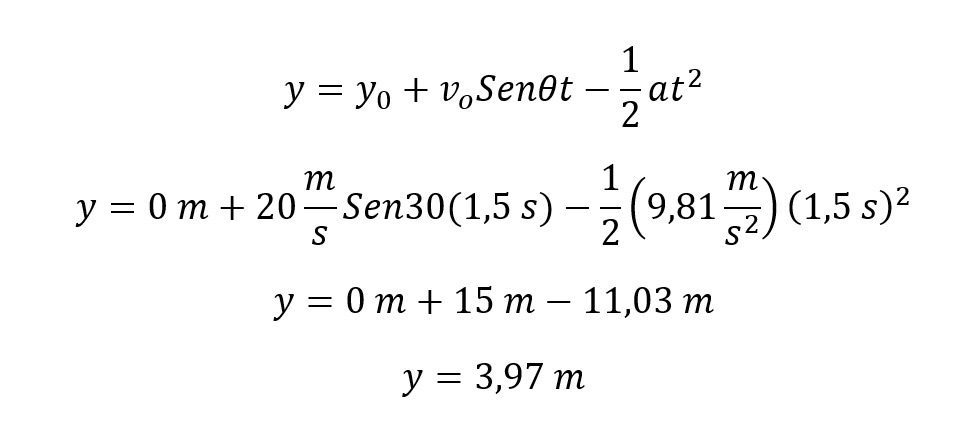



Excelente contenido!
Gracias, profe Ricardo.