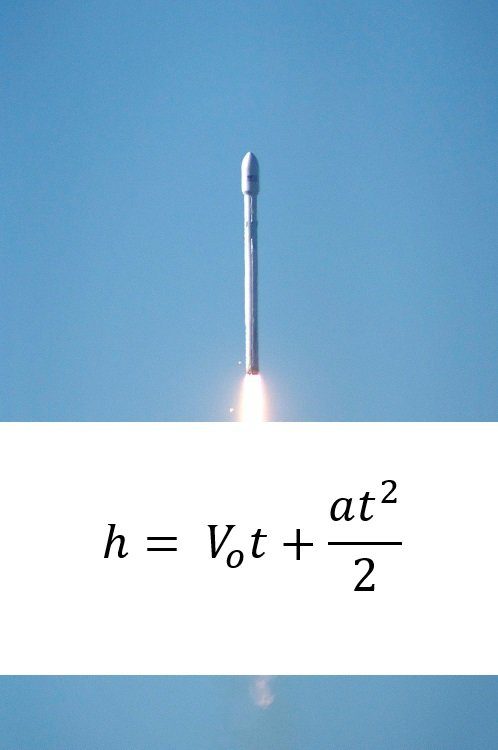El lanzamiento vertical o tiro vertical como también se le conoce es un movimiento rectilíneo uniformemente acelerado (MRUA) o movimiento rectilíneo uniformemente variado (MRUV) donde se lanza un cuerpo verticalmente con una velocidad inicial desde cierta altura y no encuentra resistencia en el recorrido.
Tabla de contenidos
Características del lanzamiento vertical
Para que un movimiento sea considerado lanzamiento vertical debe cumplir con las siguientes características:
- El lanzamiento hacía arriba puede darse desde una altura inicial que denominaremos yo este valor será igual a cero si el movimiento inicia desde el suelo, será positivo si empieza desde alguna altura determinada, por ejemplo las manos de una persona e incluso puede ser negativo si se hace el lanzamiento desde un punto bajo el suelo, por ejemplo desde lo profundo de un pozo.
- La velocidad inicial del movimiento debe ser diferente de cero, con esto se asegura que el cuerpo se eleve con el movimiento.
- La aceleración del cuerpo va a ser la gravedad, recordemos que dependiendo el lugar donde se realice el experimento este valor va a cambiar
| Lugar | Gravedad (m/s^2) |
| Luna | 1.6 |
| Mercurio | 2.8 |
| Venus | 8.9 |
| Tierra | 9.8 |
| Marte | 3.7 |
| Júpiter | 22.9 |
| Saturno | 9.1 |
| Urano | 7.8 |
| Neptuno | 11 |
- El movimiento tiene una velocidad inicial determinada que irá disminuyendo a medida que el cuerpo gana altura, el punto máximo de altura es cuando la velocidad final es igual a cero.
- El tiempo que tarda un objeto en alcanzar la altura máxima en un lanzamiento vertical es el mismo tiempo que tarda en caída libre desde la altura máxima al punto desde donde fue lanzado.
Ecuaciones de lanzamiento vertical
Recordemos que el lanzamiento vertical es una particularidad del movimiento uniformemente acelerado, por lo que las ecuaciones se deducen a partir de las ecuaciones generales.
Primera ecuación: altura en un momento determinado
La primera de las ecuaciones del movimiento uniformemente acelerado es la que describe la posición final de un cuerpo teniendo en cuenta la posición inicial, la velocidad, la aceleración y el tiempo que tarda en movimiento.
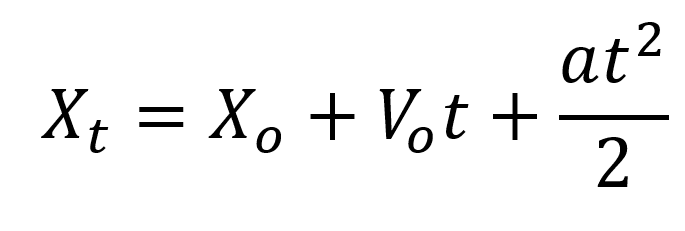
En un lanzamiento vertical la posición conocida como Xt es la distancia que va recorriendo el cuerpo, si a esa posición se le resta la posición inicial del cuerpo obtendremos la altura recorrida hasta un punto determinado, existe una posición donde el cuerpo se suspende y luego empieza a caer, esa será la altura máxima.

Teniendo en cuenta esto se puede reescribir la ecuación de posición como:
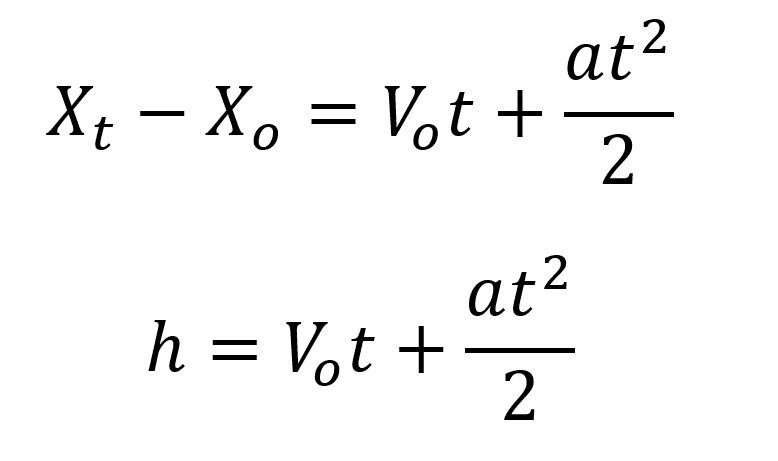
Para el caso la aceleración es igual a la gravedad.
Segunda ecuación: altura máxima respecto aceleración y velocidad inicial
En la primera ecuación se determinaba la posición del cuerpo una vez transcurrido un tiempo determinado, sin embargo si se desea conocer la altura máxima que alcanza un cuerpo no se puede determinar solo con la velocidad inicial y el tiempo, de allí nace la necesidad de utilizar la segunda ecuación del movimiento uniformemente acelerado que establece:
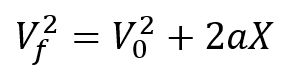
Una vez más, recordamos que en los lanzamientos verticales la velocidad final en la altura máxima es igual a cero por lo que la ecuación se puede escribir como:
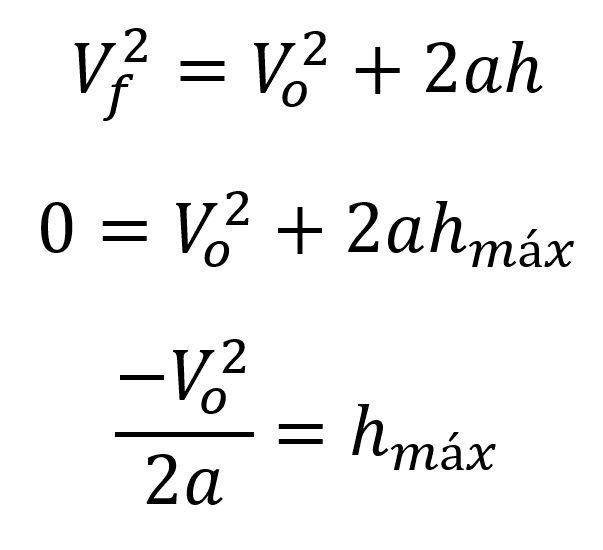
Tercera ecuación: tiempo para llegar a una altura determinada
Para determinar el tiempo que tarda un objeto en llegar a una altura determinada se debe utilizar la primera ecuación:
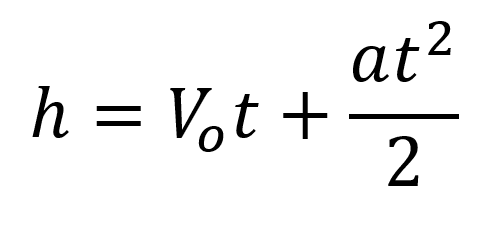
A partir de esta ecuación se debe despejar el tiempo, sin embargo vemos que aparece dos veces, un término se encuentra elevado al cuadrado y el otro no por lo que su resolución se plantea como una ecuación de segundo grado.
Lo primero es re escribir la ecuación en su forma canónica:
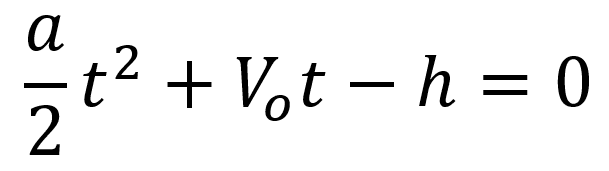
Una vez está escrita de esta manera podemos ver la similitud con la ecuación de segundo grado:
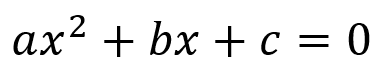
Para solucionar este tipo de ecuaciones recordamos que:
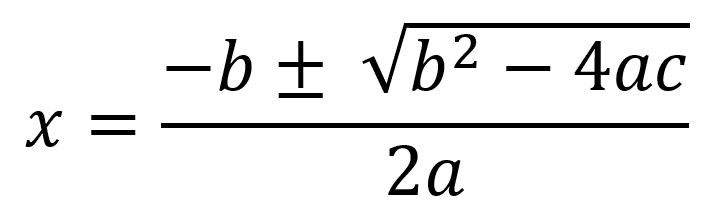
Por lo que la solución para determinar el tiempo transcurrido desde el lanzamiento vertical hasta un punto determinado es:
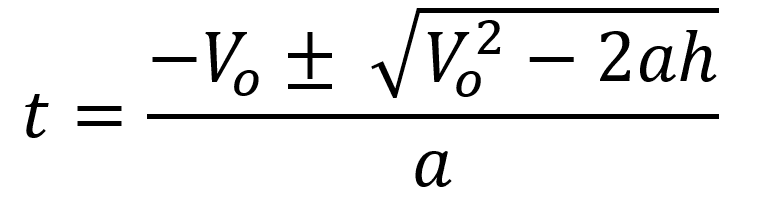
En este y en todos los casos se debe tener en cuenta que la aceleración es igual a la gravedad.
Cuarta ecuación: tiempo para llegar a la altura máxima
El lanzamiento vertical al ser una particularidad del movimiento uniformemente acelerado cumple con con las ecuaciones generales, por ello conociendo que:
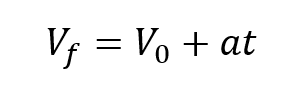
Recordando que la velocidad final en el punto de máxima altura es igual a cero:
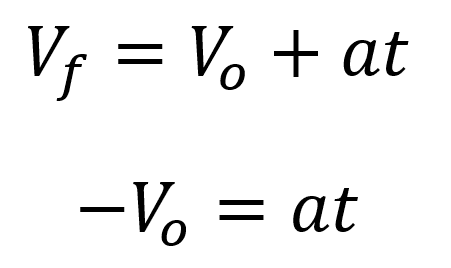
se puede concluir que el tiempo que tarda el cuerpo en alcanzar su máxima altura es:
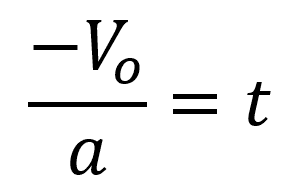
En resumen, las ecuaciones que describen el movimiento en un lanzamiento vertical son:
| Descripción | Ecuación |
| Ecuación 1. Altura en un momento determinado | 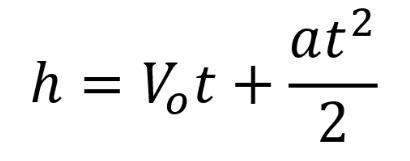 |
| Ecuación 2. Altura máxima con respecto a aceleración y velocidad inicial | 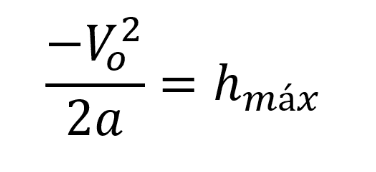 |
| Ecuación 3. Tiempo para llegar a una altura determinada | 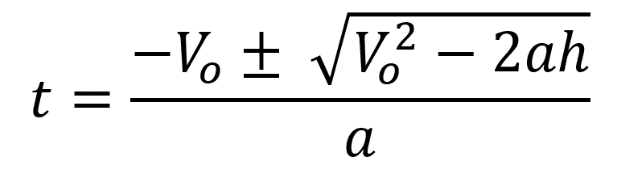 |
| Ecuación 4. Tiempo para llegar a la altura máxima | 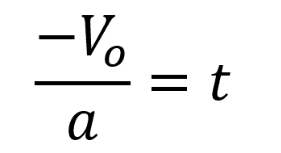 |
Errores comunes en la resolución de ejercicios de lanzamiento vertical
Antes de empezar a explicarte cómo resolver los ejercicios de lanzamiento vertical, las ecuaciones que describen el movimiento y darte ejemplos debes tener en cuenta los errores principales que se cometen cuando se estudia este tipo de movimiento:
- La aceleración que se tiene en cuenta para la resolución de los ejercicios es la gravedad, como esta actúa en contra del movimiento (la gravedad quiere llevar el cuerpo hacía abajo, el lanzamiento vertical quiere llevar el cuerpo hacía arriba) el signo debe ser negativo.
- En algunos casos se pide determinar soluciones de situaciones hipotéticas como el lanzamiento vertical de una bola en la luna o en júpiter, en estos ejemplos la gravedad no es igual a la de la tierra por lo que es necesario conocer los datos de la aceleración en estos lugares.
Ejercicios resueltos de lanzamiento vertical
Existen diferentes tipos de ejercicios que se pueden derivar de un movimiento en lanzamiento vertical, es importante a reconocer cuál es la incógnita en cada uno de ellos y así mismo identificar el procedimiento para dar solución, te explicaremos paso a paso cómo resolver cada uno de ellos dando ejemplos detallados.
Tipo de ejercicio #1: relación altura, velocidad inicial y tiempo
En este tipo de ejercicios se propone principalmente dos escenarios, el primero es encontrar la altura que alcanza un cuerpo conociendo el tiempo que tarda el lanzamiento vertical y la velocidad inicial con la que se realiza, el segundo es encontrar la velocidad inicial con la que fue lanzado el objeto si se conoce la altura que ha recorrido y el tiempo en hacerlo, vamos a ver ejemplos:
Encontrar la altura
Se lanza verticalmente un sombrero con una velocidad inicial de 50 m/s ¿Cuál será la altura luego de que han transcurrido 2 segundos?
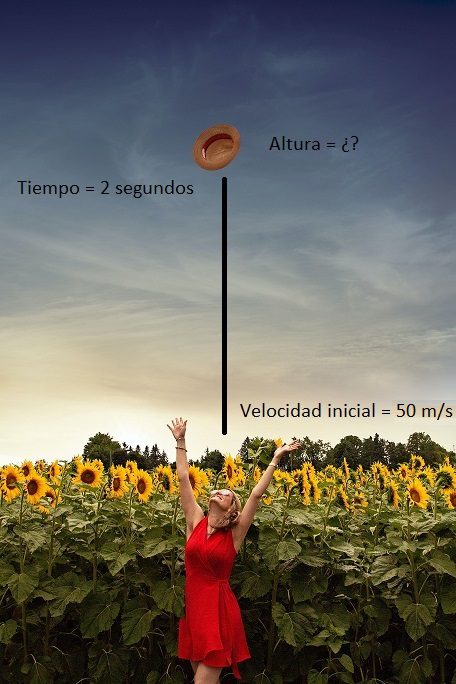
Solución:
Lo primero que se debe tener en cuenta para la resolución de los ejercicios es la identificación de los datos que se conocen y la incógnita que se pregunta, para este caso se conoce la velocidad inicial, el tiempo transcurrido y la aceleración (que es la gravedad de la tierra 9.81 m/s2) pero se desconoce el tiempo que precisamente es el dato por el que nos preguntan, la ecuación que relaciona todas las variables es:
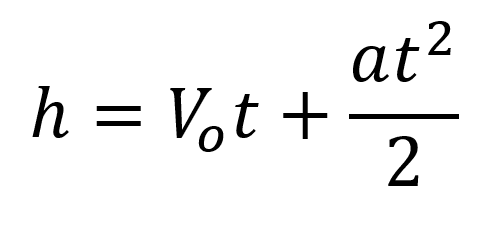
Se reemplazan los valores conocidos y se procede a realizar las operaciones necesarias, es necesario recordar dos cosas, la primera es que la gravedad está en contra de la dirección del movimiento por lo que el signo de la aceleración es negativo y segundo que como se está preguntando una altura la respuesta debe estar en metros que son las unidades acordes.
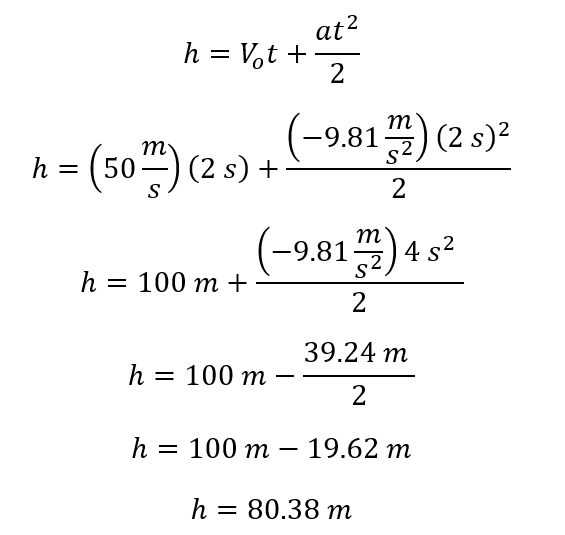
De este modo se establece que después de 2 segundos el sombrero se encuentra a una altura de 80.38 metros.
Posibles aspectos a tener en cuenta:
En algunas ocasiones se plantean ejercicios para determinar la comprensión del estudiante frente a la temática desarrollada y se suelen poner ciertas «trampas» por parte de los profesores como por ejemplo en el siguiente caso:
Imaginemos el mismo ejercicio anterior pero en lugar de que el sombrero sea lanzado a 50 m/s esta vez será lanzado a 2 m/s, después de 2 segundos se quiere conocer su altura.
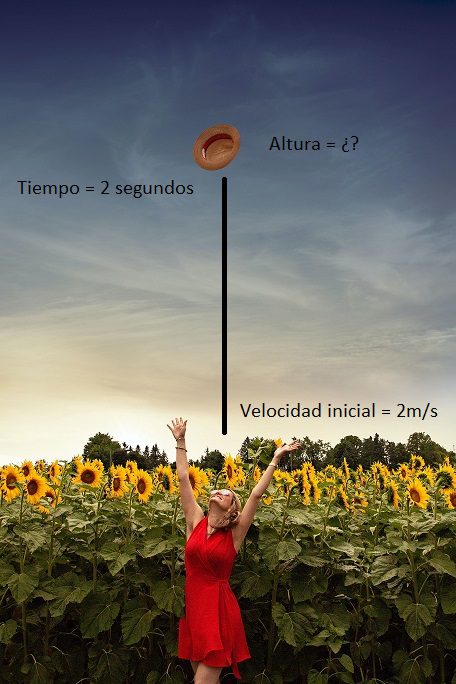
El procedimiento para resolver es exactamente el mismo, en este caso:
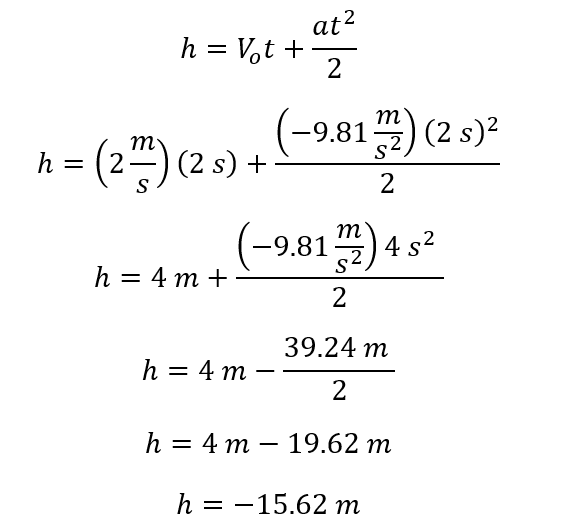
Debes tener cuidado con este tipo de ejercicio donde al final encontramos que la altura es negativa -15.62 m, cuando suceden estos casos lo que significa es que la velocidad inicial con la que es lanzado verticalmente el objeto no es lo suficiente para mantenerlo en el aire después del tiempo transcurrido, es decir como en el ejemplo de la foto si se lanzara el sombrero a 2 m/s después de 2 segundos nuevamente estaría en el suelo.
Encontrar la velocidad inicial
¿Con que velocidad debe lanzar la gimnasta el balón para que una vez han transcurrido 0.35 segundos este alcance una altura de 70 centímetros?

Lo primero que debemos hacer es transformar todas las unidades al sistema internacional, en este caso recordemos que no se trabaja con centímetros sino con metros por lo que se hace la conversión:
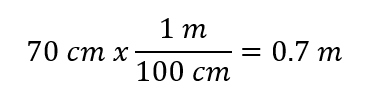
Una vez tenemos todos los datos en el sistema internacional de medidas procedemos a reemplazar los valores conocidos y despejar la incógnita que en este caso es la velocidad inicial.

La velocidad inicial con la que debe lanzar el balón es de 3.72 m/s para que alcance una altura de 70 centímetros en 0.35 segundos.
Tipo de ejercicio #2: relación altura máxima y velocidad inicial.
En este tipo de ejercicios se pueden platear básicamente dos escenarios.
El primero de ellos es encontrar la altura máxima que alcanza un objeto cuando es lanzado a determinada velocidad inicial.
El segundo es el de encontrar la velocidad inicial con la que fue lanzado cuando llega a una altura máxima en un lanzamiento vertical.
Tranquilo, creemos que con un ejemplo todo es mucho más fácil.
Encontrar altura máxima
¿Cuál es la altura máxima que alcanza una pelota de tenis que es golpeada y sale a una velocidad inicial de 5 m/s?

Lo primero que se debe saber es cuál de las ecuaciones nos relaciona los datos suministrados en el ejercicio.
Para este caso donde se necesita conocer la altura máxima se cuenta con la ecuación:
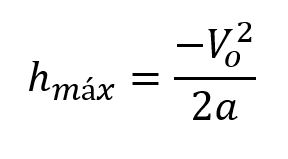
Una vez se conoce la ecuación se proceden a reemplazar los valores conocidos y encontrar el valor de la incógnita.
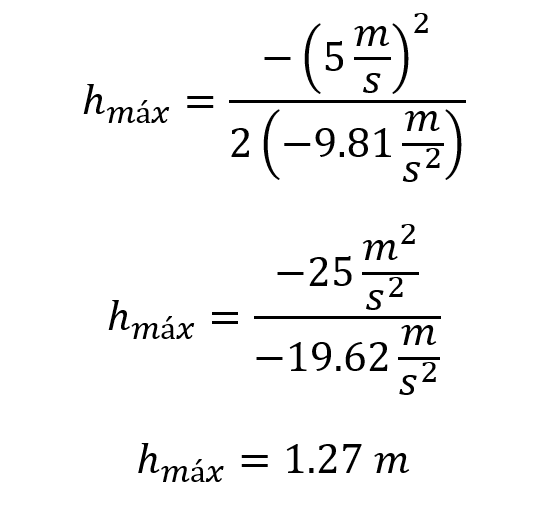
En este caso la altura máxima que alcanza la pelota es de 1.27 metros cuando es lanzada a una velocidad inicial de 5 m/s
Encontrar la velocidad inicial conociendo la altura máxima
Un par de niñas lanzan unas hojas verticalmente y estas alcanzan una altura máxima de 1.8 metros
¿Cuál fue la velocidad inicial con que fueron lanzadas las hojas?

Una vez más nos encontramos con un ejercicio donde se relaciona la altura máxima con la velocidad inicial solo que en esta ocasión la incógnita es diferente, sin embargo es perfectamente válido utilizar la ecuación:
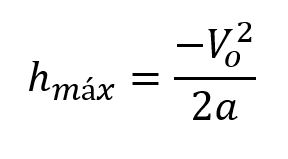
Se reemplazan los valores conocidos y se procede a solucionar.

La velocidad con la que fueron lanzadas las hojas para que llegaran a una altura máxima de 1.8 metros es de 5.94 m/s
Tipo de ejercicio #3: relación tiempo, altura y velocidad inicial.
En este tipo de ejercicios se busca determinar el tiempo que un cuerpo tarda en llegar a una altura (no es la máxima) dadas la velocidad inicial y aceleración.
Por ejemplo:
Un cohete despega verticalmente a una velocidad inicial de 200 m/s ¿Cuánto tiempo tardará en alcanzar una altura de 500 metros?

Para este caso se utiliza la ecuación:
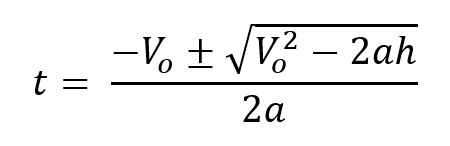
Se reemplazan los valores conocidos:
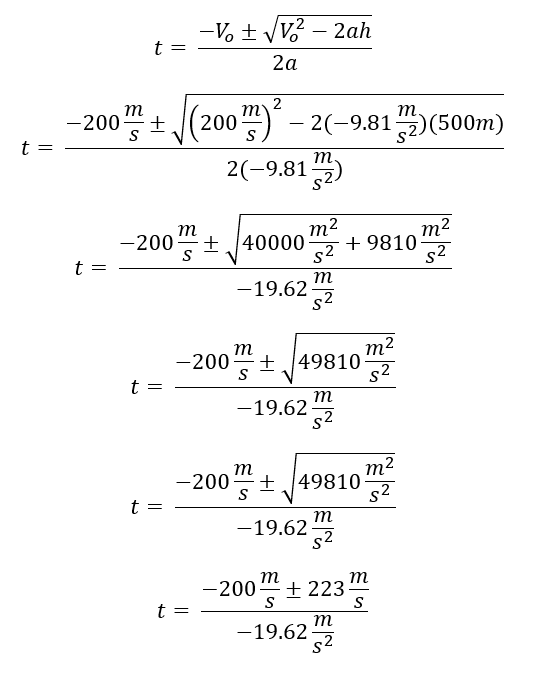
En este punto como tenemos un signo ± se deben plantear dos soluciones primero realizando la suma y luego realizando la resta. Empecemos con la suma:
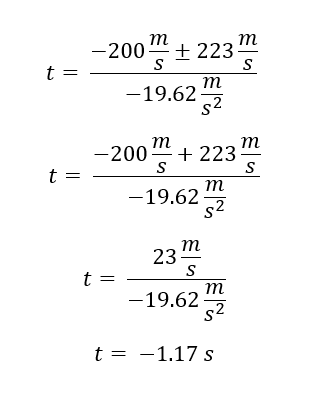
Como el tiempo no puede ser negativo para que el cohete alcance la altura deseada se utiliza la resta:
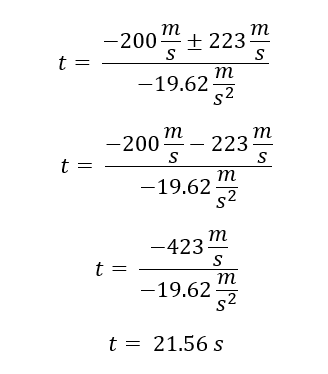
De este modo se establece que con una velocidad inicial de 200 m/s el cohete tarda 21.56 segundos en alcanzar una altura de 500 metros.
Tipo de ejercicio #4: relación tiempo, altura máxima y velocidad inicial.
Sin duda alguna este es el más sencillo de los casos que se pueden presentar.
En este tipo de ejercicios se suele determinar el tiempo que tarda un cuerpo en alcanzar la altura máxima con base en su velocidad inicial, por ejemplo:
¿Cuánto tiempo tarda en alcanzar la altura máxima una cámara fotográfica que es lanzada verticalmente si la velocidad inicial con que se arrojo fue de 10 m/s?

Para este caso se utiliza la ecuación:
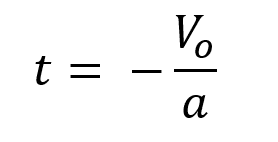
Se reemplazan los valores conocidos y se despeja:
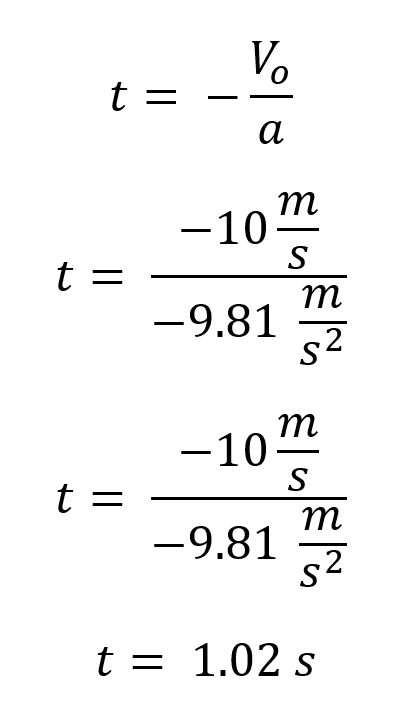
El tiempo que tarda la cámara en alcanzar la altura máxima es de 1.02 segundos.
¿Cómo referenciarnos?
Si deseas incluir esta información en alguno de tus trabajos no olvides referenciarnos, puedes hacerlo así:
Munévar, R. (7 de abril de 2024) Lanzamiento Vertical. Ecuacionde.com. Recuperado el día/mes/año (inserta aquí la fecha del día que consultas nuestra web) de https://ecuacionde.com/lanzamiento-vertical