La caída libre se define como aquel movimiento que se da en un cuerpo únicamente por la influencia de la gravedad, inicialmente, en el estudio de este tipo de movimiento no se tiene en cuenta la resistencia del aire, de allí la afirmación de Galileo hace más de 400 años donde afirma que una pluma y un martillo caen a la misma velocidad si el experimento se realiza en el vacío.

Tabla de contenidos
Leyes fundamentales de la caída libre
Antes de continuar se deben dejar claras las condiciones que se deben tener en cuenta para que un movimiento se considere caída libre, estas condiciones se conocen como las leyes fundamentales de la caída libre y son:
- Todos los cuerpos que tengan una caída libre tienen una trayectoria estrictamente vertical, no hay desviación en el recorrido de ningún tipo.
- La caída libre de los cuerpos es un caso del movimiento uniformemente acelerado.
- Todos los cuerpos caen con la misma aceleración si se dejan caer en el mismo lugar porque la única influencia es la gravedad.
- Todos los cuerpos que se dejan caer en el vacío se demoran el mismo tiempo en alcanzar la misma velocidad.
Ecuaciones de caída libre
Recordemos que la caída libre es una particularidad del movimiento uniformemente acelerado, por lo que las ecuaciones se deducen a partir de las ecuaciones generales.
Primera ecuación: posición final
La primera de las ecuaciones del movimiento uniformemente acelerado es la que describe la posición final de un cuerpo teniendo en cuenta la posición inicial, la velocidad, la aceleración y el tiempo que tarda en movimiento.
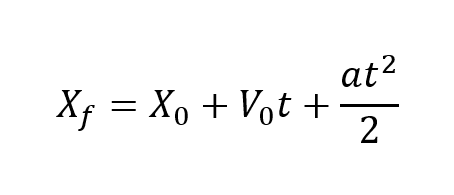
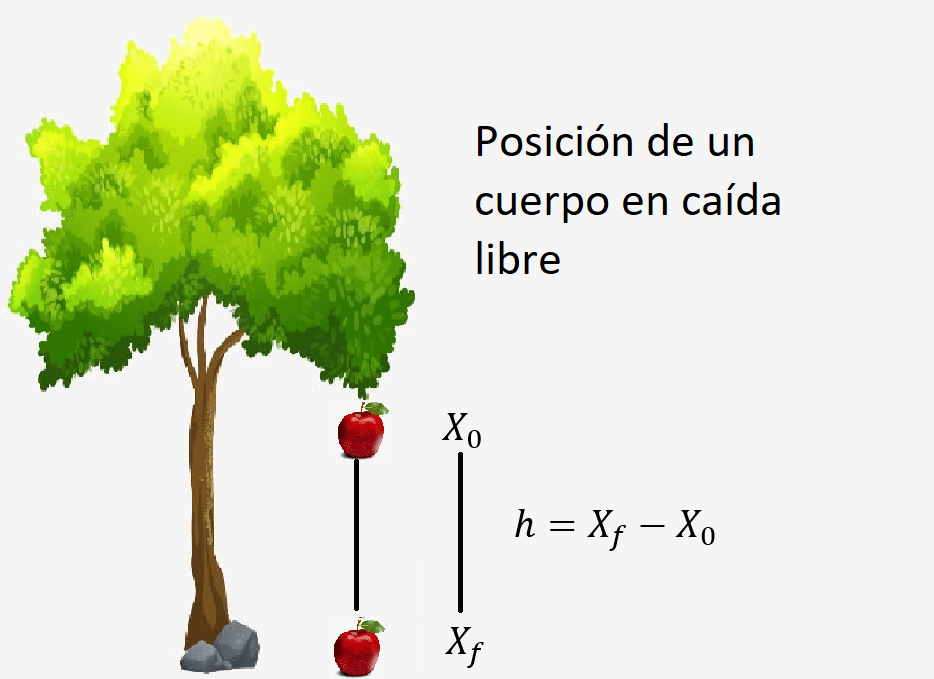
En una caída libre la posición inicial menos la posición final del cuerpo equivale a la altura desde la cual empieza a caer el cuerpo.
Teniendo en cuenta esto se puede reescribir la ecuación de posición como:
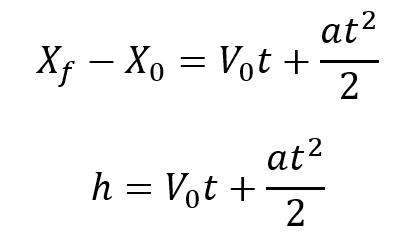
Como en la caída libre el cuerpo no se ve afectado por ninguna fuerza externa sino únicamente por la gravedad la velocidad inicial es cero por lo que la ecuación quedaría:
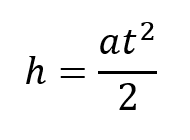
Segunda ecuación: velocidad final respecto a aceleración y tiempo
Para determinar la velocidad final con la que un objeto golpea el suelo se utiliza la ecuación
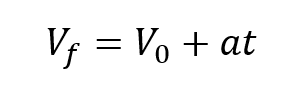
Sin embargo como se había mencionado anteriormente en la caída libre la velocidad inicial en los movimientos de caída libre es igual a cero por lo que la velocidad final es igual a:
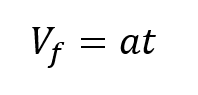
Tercera ecuación: velocidad final respecto aceleración y posición
En la segunda ecuación se determinaba la velocidad final teniendo en cuenta la aceleración y el tiempo de caída libre, sin embargo en algunas ocasiones no se conoce el tiempo de la caída sino solo la posición, de allí nace la necesidad de tener una tercera ecuación que establece:
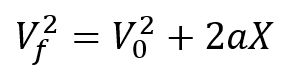
Una vez más, recordamos que en la caída libre la velocidad inicial es igual a cero por lo que:
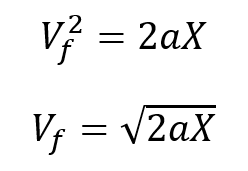
Teniendo esto en cuenta, las ecuaciones que describen el movimiento de caída libre son:
| Descripción | Ecuación |
| Ecuación 1. Posición final | 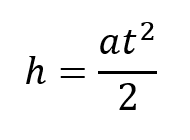 |
| Ecuación 2. Velocidad final (con tiempo) | 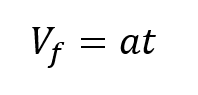 |
| Ecuación 3. Velocidad final (con posición) | 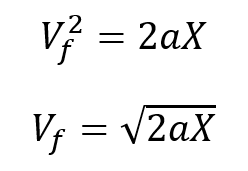 |
Errores comunes en la resolución de ejercicios de caída libre
Antes de empezar a explicarte cómo resolver los ejercicios de caída libre, las ecuaciones que describen el movimiento y darte ejemplos debes tener en cuenta los errores principales que se cometen cuando se estudia este tipo de movimiento:
- Cuando se hace un análisis de caída libre algunas personas tienden a pensar que la velocidad final es cero porque el objeto termina quieto en el piso, sin embargo esto NO es así, la velocidad final en los ejercicios de física es la que tiene el cuerpo justo antes de tocar el suelo.
- En algunos casos se pide determinar soluciones de situaciones hipotéticas como la caída de un martillo en la luna o en júpiter, en estos ejemplos la gravedad no es igual a la de la tierra por lo que es necesario conocer los datos de la aceleración en estos lugares.
La gravedad: aceleración en la caída libre
Debido a que la caída libre se da únicamente por la influencia de la gravedad es importante que se conozca ese valor, no solo para el planeta tierra sino para todos los planetas del sistema solar, en algunos casos se pueden presentar ejercicios como ¿a qué velocidad cae un astronauta luego de saltar en la luna? o ¿cuál es la velocidad con la que un satélite cae sobre la superficie de Júpiter? para esto te presentamos la gravedad de los planetas del sistema solar:
| Lugar | Gravedad (m/s^2) |
| Luna | 1.6 |
| Mercurio | 2.8 |
| Venus | 8.9 |
| Tierra | 9.8 |
| Marte | 3.7 |
| Júpiter | 22.9 |
| Saturno | 9.1 |
| Urano | 7.8 |
| Neptuno | 11 |
Ejercicios resueltos de caída libre
Existen diferentes tipos de ejercicios que se pueden derivar de un movimiento en caída libre, es importante a reconocer cuál es la incógnita en cada uno de ellos y así mismo identificar el procedimiento para dar solución, te explicaremos paso a paso cómo resolver cada uno de ellos dando ejemplos detallados.
Tipo de ejercicio # 1: relación altura, aceleración y tiempo
Este tipo de ejercicio propone calcular la altura desde la cual se deja caer un objeto cuando se conoce el tiempo que tardó en hacer el recorrido, algunos ejemplos serían:
Ejemplo 1:
Se deja caer una piedra desde lo alto de un edificio y tarda 4,5 segundos en tocar el suelo, ¿Qué altura tiene el edificio?
Solución
Lo primero que se debe reconocer en un ejercicio son los datos que este ofrece, para el caso se conoce el tiempo (4,5 s) e implícitamente se conoce la aceleración, al ser una caída libre en el planeta tierra la gravedad (aceleración) es 9.8 m/s^2 y la incógnita es la altura del edificio.
La ecuación 1. Posición final relaciona todas las variables que tenemos en el ejercicio por lo que procedemos a utilizarla y resolverla así:
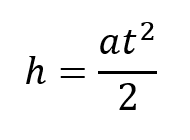
Se reemplazan los valores:
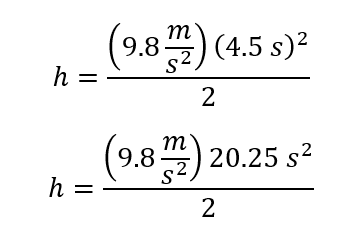
En este caso al multiplicar la aceleración por el tiempo al cuadrado se puede observar que las unidades de segundo al cuadrado se cancelan por lo que queda:
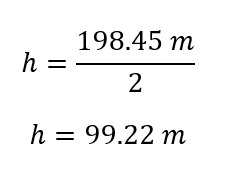
En este caso la altura del edificio son 99,22 metros.
Ejemplo 2:
¿Cuánto tiempo tarda en caer un balón desde un edificio de 98 metros de altura?
Solución:
Al igual que en el ejemplo anterior se deben identificar los datos conocidos, en este caso se tiene la altura del edificio (98 metros) y la aceleración (gravedad) que es de 9,8 m/s^2 la incognita para este ejercicio es el tiempo.
La ecuación 1. Posición final relaciona todas las variables que tenemos en el ejercicio por lo que procedemos a utilizarla y resolverla así:
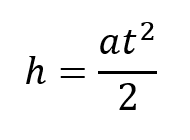
Se reemplazan los valores:
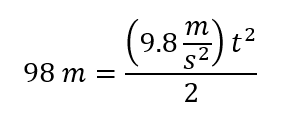
y se despeja la variable tiempo:
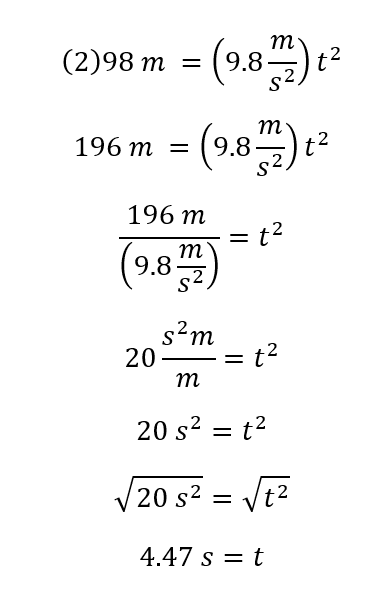
Tipo de ejercicio # 2: relación velocidad final, aceleración y tiempo.
En este tipo de ejercicios se suele preguntar la velocidad final de caída de un objeto o cuánto tarda un cuerpo en alcanzar una velocidad determinada, algunos ejemplos son:
Ejemplo:
¿Cuál es la velocidad final con la que una piedra golpea el piso si estuvo en caída libre por 12 segundos?
Solución:
Como en todos los ejercicios se determinan cuales son las variables conocidas, en este caso el tiempo de caída de la piedra (12 segundos) y la aceleración que está implícita 9,8 m/s^2.
La Ecuación 2. Velocidad final (con tiempo) relaciona todas las variables que tenemos en el ejercicio por lo que procedemos a utilizarla y resolverla así:
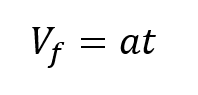
Se reemplazan valores
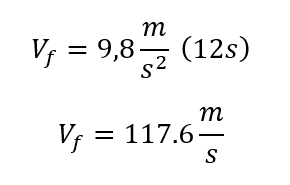
La velocidad final con la que la piedra golpea el piso es de 117.6 m/s
Otro ejemplo que se puede presentar en este tipo de ejercicio es:
Ejemplo 2:
Se deja caer un cuerpo en la Luna hasta que alcanza una velocidad de 40m/s ¿Cuánto tiempo tarda en alcanzar esta velocidad?
Solución:
En este caso las variables conocidas son la velocidad final de 40 m/s y la aceleración en la luna que se encuentra en la tabla y es de 1.6 m/s^2.
La Ecuación 2. Velocidad final (con tiempo) relaciona todas las variables que tenemos en el ejercicio por lo que procedemos a utilizarla y resolverla así:
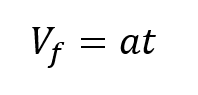
Se reemplazan valores
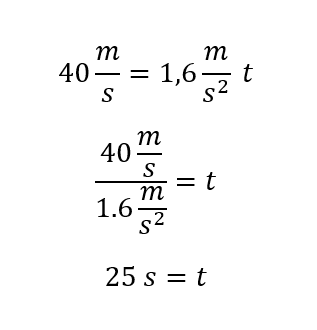
El tiempo que tarda en alcanzar los 40 m/s en la luna es de 25 segundos.
Tipo de ejercicio # 3: relación velocidad final, aceleración y posición.
En este tipo de ejercicios teniendo en cuenta la velocidad final de un cuerpo en caída libre, la aceleración o la posición se busca encontrar información que permita encontrar la incógnita deseada, algunos ejemplos son:
Ejemplo 1:
La llegada de un satélite a la superficie de marte falla y este empieza a caer en caída libre desde 5000 metros de altura ¿con qué velocidad golpeará la superifice?
Solución:
En este tipo de ejercicios se cuenta con la información sobre la posición e indirectamente con la aceleración que para el caso de marte es su gravedad 3.7 m/s^2 teniendo estos datos se utiliza la Ecuación 3. Velocidad final (con posición) así:
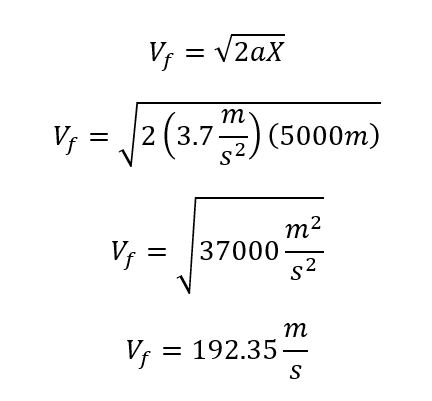
Hay algunos ejercicios de lanzamiento vertical donde después de que llega al punto máximo de altura el cuerpo sigue el procedimiento como caída libre.
Si llegas a tener alguna duda acerca de la resolución de los ejercicios, quieras que hablemos sobre algún tema en específico o simplemente para dar un saludo puedes hacerlo en los comentarios.