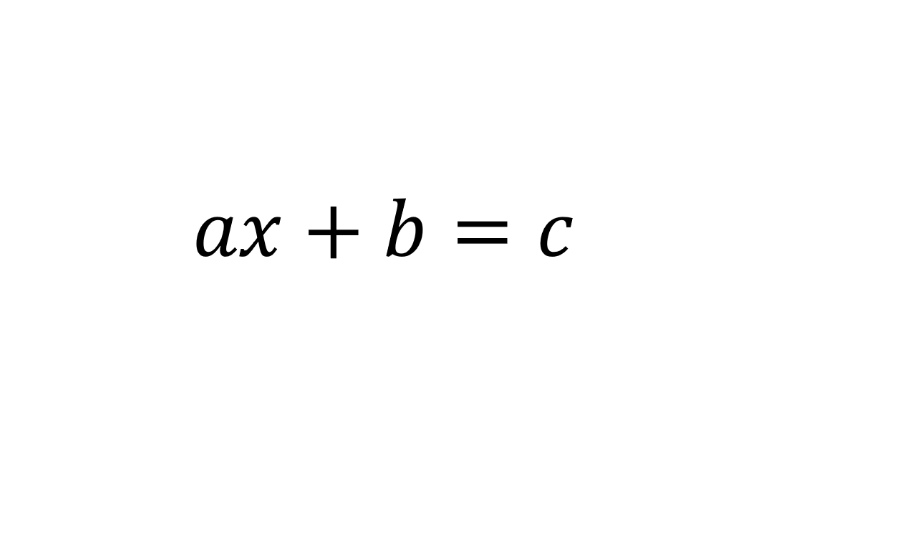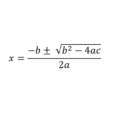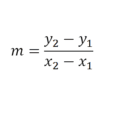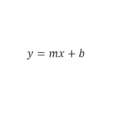Tabla de contenidos
¿Qué es una ecuación de primer grado o lineal?
En definición una ecuación de primer grado o ecuación lineal es una igualdad algebraica donde las incógnitas (o incógnita) se encuentran a la primera potencia y no hay multiplicación entre ellas, es decir una ecuación que solo presenta sumas y restas entre las variables cuando estas están a la primera potencia.
Ecuación de primer grado o lineal con una incógnita
Las ecuaciones de primer grado de con una incógnita o una variable son todas aquellas que cumplen con la forma:
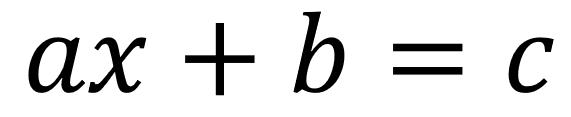
a debe ser diferente de cero
b y c son dos constantes, es decir números fijos
x es la variable o incógnita, el valor que no conocemos.
Cuando se habla de solucionar una ecuación de primer grado con una incógnita se hace referencia a encontrar el valor de x.
Ejemplos de ecuación de primer grado o lineal con una incógnita
Para ser ecuaciones de primer grado con una incógnita deben cumplir con la forma general, a continuación te presentamos varios ejemplos de ecuaciones con estas características
Ejemplo 1 de ecuación de primer grado o lineal con una incógnita
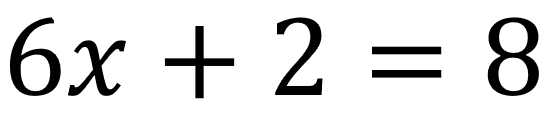
Esta ecuación cumple con todas las condiciones para ser de primer grado con una incógnita, en este caso:
a=6
b=2
c=8
Ejemplo 2 de ecuación de primer grado o lineal con una incógnita
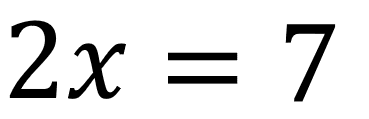
Esta ecuación cumple con todas las condiciones para ser de primer grado con una incógnita, en este caso:
a=2
b=0
c=7
Como no tiene un número sumando después de la incógnita significa que b es igual a cero ya que 2x+0 = 2x
Ejemplo 3 de ecuación de primer grado o lineal con una incógnita
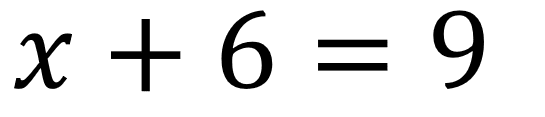
Esta es una ecuación con dos términos independientes enteros y cumple con todas las condiciones para ser de primer grado con una incógnita, en este caso:
a=1
b=6
c=9
Como x no tiene un número que lo acompañe a es igual a uno ya que 1x = x
Ejemplo 4 de ecuación de primer grado o lineal con una incógnita
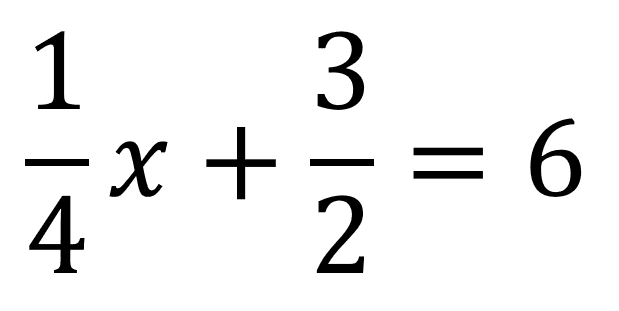
Esta ecuación cumple con todas las condiciones para ser de primer grado con una incógnita, en este caso:
a=1/4
b=3/2
c=6
Los números fraccionarios también cumplen con las condiciones para que la ecuación sea de primer grado.
EJEMPLO 5 DE ECUACIÓN DE PRIMER GRADO o lineal CON UNA INCÓGNITA
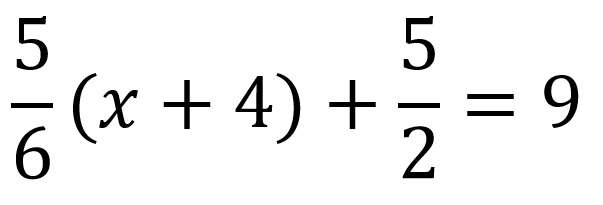
Esta ecuación cumple con todas las condiciones para ser de primer grado con una incógnita, en este caso:
a=5/6
b=35/6 (si quieres saber cómo se llegó a este valor más abajo encontrarás la explicación)
c=9
Las ecuaciones de primer grado pueden tener fraccionarios y paréntesis, el resultado de b se obtiene al solucionar la ecuación, no te preocupes que más adelante te enseñaremos como hacerlo, es muy fácil.
Ecuación lineal con dos o más incógnitas
Las ecuaciones de primer grado de primer grado con dos incógnita o dos variable son todas aquellas que cumplen con la forma:
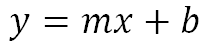
donde
y es una incógnita o valor desconocido
x es una incógnita o valor desconocido
m y b son dos constantes, es decir números fijos
También se pueden tener ecuaciones de primer grado con más incógnitas como se ve a continuación
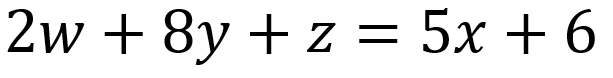
¿Qué NO es una ecuación de primer grado?
Si una ecuación presenta multiplicación entre las variables o un exponente diferente en cualquiera de las incógnitas automáticamente deja de ser de primer grado, por ejemplo:
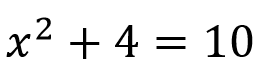
Como el exponente que tiene la incógnita es 2 esta ecuación se considera una ecuación de segundo grado.
Estos son otros ejemplos de ecuaciones que NO son de primer grado
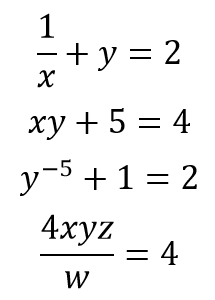
Partes de la ecuación
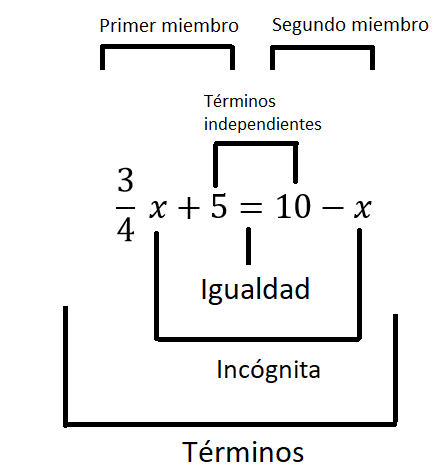
Una ecuación está compuesta por varias partes, estas partes se conocen como elementos de ecuación de primer grado y son:
- Términos
- Términos independientes
- Igualdad
- Miembros
- Incógnitas
Se encuentran de la siguiente forma
¿Cómo resolver una ecuación de primer grado?
El procedimiento para resolver una ecuación es sencillo solo depende si tiene paréntesis o denominadores, los pasos son:
- Resolver los paréntesis
- Quitar los denominadores
- Agrupar las variables x en un miembro y las variables independientes en otro
- Reducir términos semejantes
- Despejar la incógnita
Ecuaciones de primer grado con paréntesis
Existen ocasiones en las que las ecuaciones de primer grado tienen paréntesis junto con la variable o incluso fuera de ella, independiente sea el caso es necesario «romper» el paréntesis, es decir aplicar la propiedad distributiva que consiste en multiplicar el número fuera del paréntesis por cada uno de los términos de adentro, por ejemplo, encontrar la solución de x:
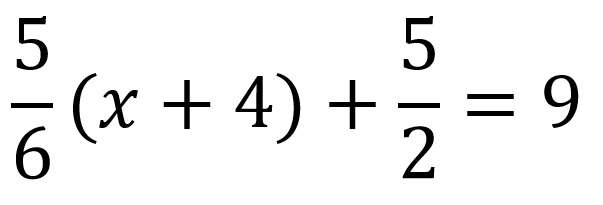
En este caso se tiene una ecuación con un solo paréntesis, el primer paso es aplicar la propiedad distributiva quedando así:
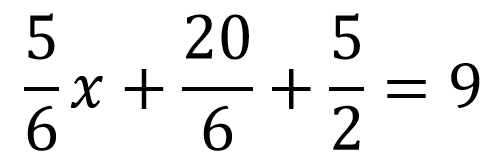
Recuerda que cuando se multiplica 5/6 por 4 se multiplica el numerador con el número entero y se mantiene el mismo denominador, es decir 5 x 4 / 6 equivalente a 20/6.
Luego de esto se deben sumar los fraccionarios que no tienen una x multiplicándolos, en este caso se deben sumar 20/6 y 5/2, para poder hacerlo se deben igualar los denominadores por lo que 5/2 se escribirá como 15/6 que es un fraccionario equivalente.
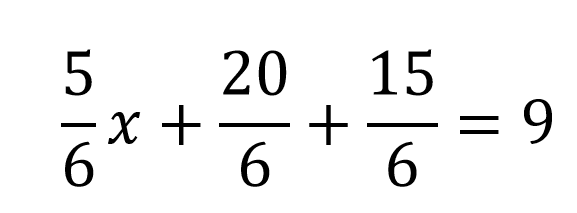
Una vez tienen el mismo denominador se suman y quedaría:
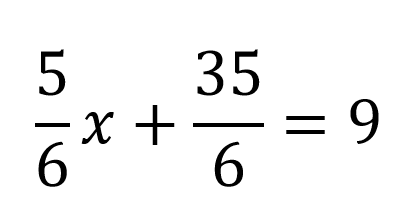
Ahora se agrupan los términos que no tienen x separados de los que sí tienen, como al 35/6 lo antecede un signo positivo pasa al otro lado del igual con signo negativo, quedando así:
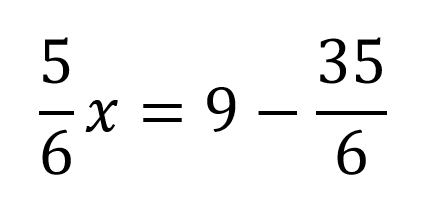
Nuevamente se igualan los denominadores para poder hacer la resta teniendo:
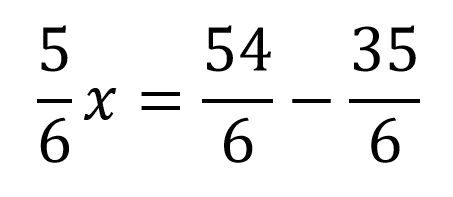
Se resuelve la resta:
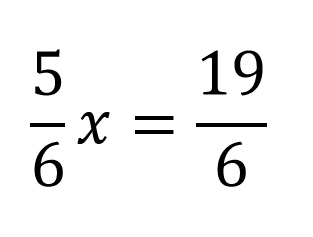
Como en ambos lados la ecuación se encuentra dividida entre 6 se pueden cancelar los denominadores quedando:
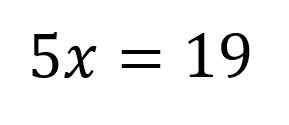
Finalmente se despeja x, como 5 está multiplicando pasa al otro lado a dividir:
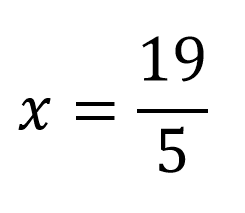
Encontrando así el valor de la incógnita.
Ecuaciones de primer grado con paréntesis antecedidos por un signo negativo
Es importante recalcar que los paréntesis hacen que las ecuaciones tomen otro significado y más cuando se tiene un signo negativo antes del mismo ya que hace que todos los signos cambien, por ejemplo, encontrar el valor de x:
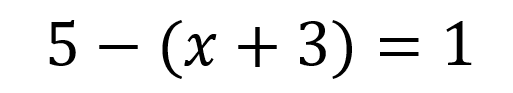
Como vimos en el ejemplo anterior el primer paso es «romper el paréntesis» como hay un signo negativo antes se deben cambiar los signos dentro del paréntesis quedando así:
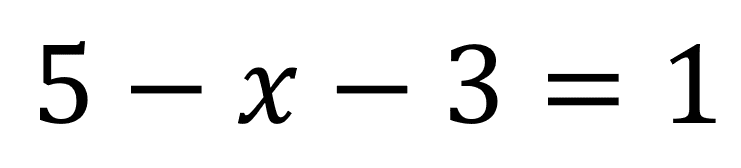
Luego de esto se agrupan los términos que tienen x, a un lado del igual y los que no tienen al otro lado así:
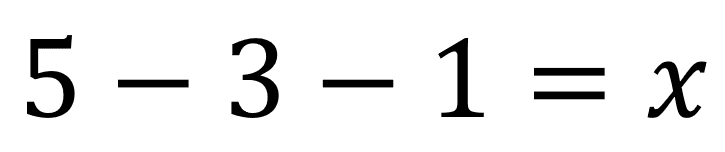
Recuerda que el signo de la x cambió porque se pasó al otro lado del igual, así como el 1.
Finalmente,
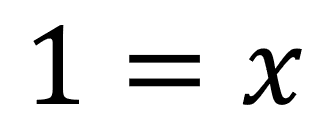
Ecuaciones de primer grado con denominadores
En muchos casos se presentan denominadores cuando requerimos solucionar ecuaciones de primer grado, recuerda que para ser una ecuación de primer grado la incógnita siempre está en el númerador. Por ejemplo, resolver:
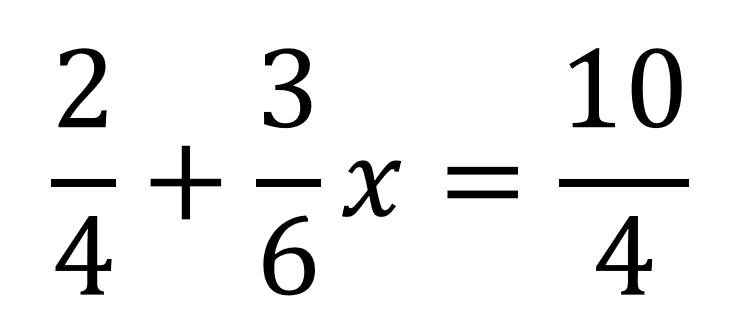
En esta ecuación tenemos tres fraccionarios, uno de ellos acompañando a la x y los otros dos sin incógnita, el primer paso es separar a un lado del igual los que tienen incógnita y al otro lado los que no.
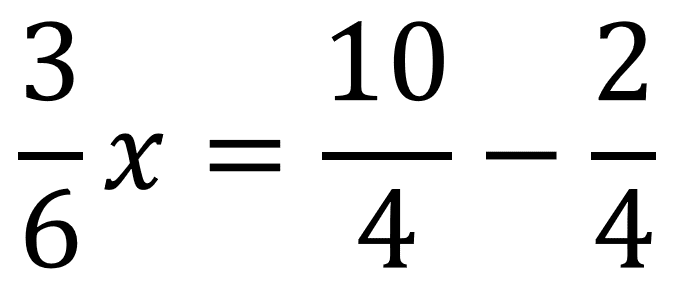
Una vez se tienen separados los términos se procede a hacer la operación de los dos fraccionarios que quedaron a la derecha del igual, en este caso como tienen el mismo denominador este valor se mantiene y se restan los numeradores quedando:
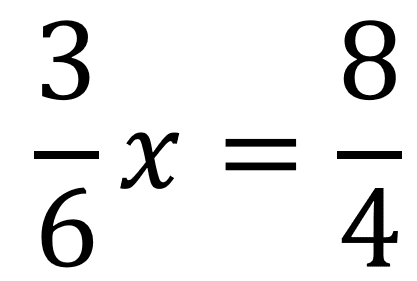
Debido a que 8 se puede dividir entre 4 y da un número exacto se procede a realizar la simplificación de ese fraccionario y se obtiene:
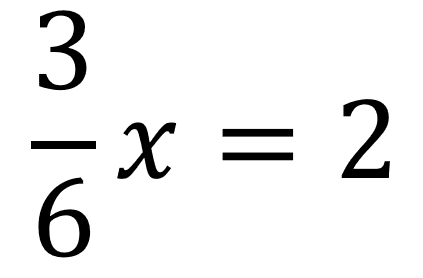
Para despejar la x se requiere pasar al otro lado del igual el fraccionario que lo acompaña, en este caso como el 6 está dividiendo pasa a multiplicar, mientras que el 3 que está multiplicando pasa a dividir, quedando:
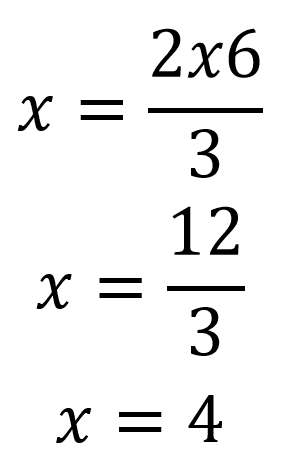
Para el ejercicio que se planteó el valor de x es 4.
¿Qué significa que la solución de una ecuación me de 0 = 0?
Cuando en una ecuación de primer grado se obtiene como resultado 0=0 significa que dicha ecuación tiene infinitas soluciones, es decir independiente del valor de la incógnita la igualdad siempre se va a mantener, por ejemplo:
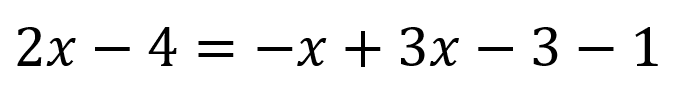
El primer paso para resolver la ecuación es ubicar los términos que tienen x a un lado y al otro los que no tienen, quedando:
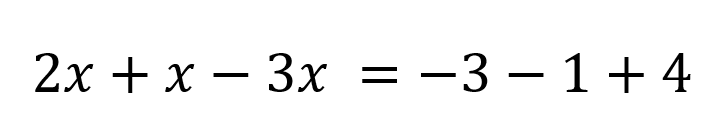
En este caso cuando se hace la operación tanto a la izquierda como a la derecha de la ecuación se tiene que 2x+x-3x = 0 y -3 -1 + 4 = 0 por lo que se tiene una igualdad 0=0, es decir que tiene infinitas soluciones independiente del valor que se le de a la incógnita, por ejemplo si se asigna un valor de x = 10:
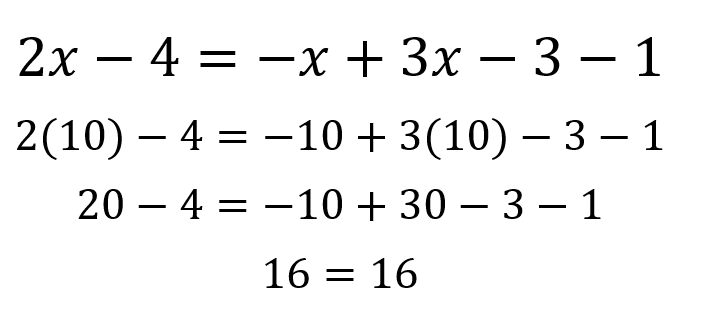
Así mismo sucede si por ejemplo se reemplaza x = 3:

Independientemente del valor que se le asigne a la x siempre se va a cumplir la igualdad cuando una ecuación de primer grado tiene la forma 0=0.
¿Qué significa que la solución de una ecuación me de 0 = otro valor?
Cuando en una ecuación de primer grado se obtiene como resultado 0= otro valor significa que dicha ecuación no tiene soluciones, es decir independiente del valor que se le asigne a la incógnita nunca va a existir una igualdad, por ejemplo:
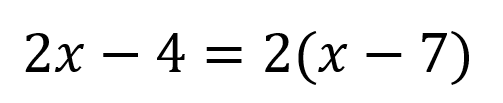
Como se vio anteriormente en las ecuaciones de primer grado con paréntesis el primer paso es quitar dicho paréntesis utilizando la propiedad asociativa así:
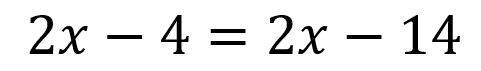
Luego se agrupan los términos que tienen x a un lado de la igualdad y los que no al otro, quedando:
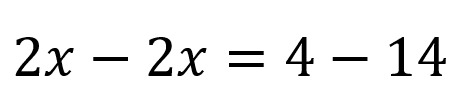
Al resolver se tiene que:
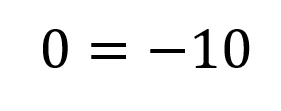
En ningún caso y bajo ninguna circunstancia 0=-10 por lo que no existe ningún valor de x que permita hacer esta igualdad.