La ley de Hooke o ley de elasticidad es el principio físico que determina la elasticidad en los sólidos, el caso más común de su aplicación es en el estudio de los resortes, sin embargo, se puede aplicar también en diferentes materiales como barras de metal, piezas de concreto y segmentos plásticos.
Tabla de contenidos
Historia
La ley de Hooke fue formulada en el año 1660 por Robert Hooke, establece que la deformación elástica que sufre un cuerpo es proporcional a la fuerza que produce tal deformación, siempre que no se sobrepase el límite de elasticidad.
En la época se estaban desarrollando grandes descubrimientos científicos liderados principalmente por los avances en el cálculo propuesto por Isaac Newton, por lo que la comprensión del comportamiento de los fenómenos elásticos representaba un gran avance en materia de ciencia.
Hooke estudió profundamente la elasticidad que es la capacidad de un cuerpo para recuperar su forma y tamaño original luego de ser comprimido o estirado por una fuerza externa, lo hizo a través de la elaboración de piezas en su trabajo de metalurgia.
El famoso anagrama de Hooke
Cuando publicó los resultados de sus investigaciones Robert Hooke lo hizo en forma de anagrama para evitar que alguien más se apropiase de la idea, inicialmente lo hizo como ceiiinosssttuv, posteriormente cuando los resultados se hicieron definitivamente públicos el anagrama fue ordenado y se podía leer en latín Ut tensio sic vis, que traduce, como la extensión, así la fuerza haciendo relación a aplicación matemática de su ley.
Aplicaciones de la ley de Hooke
La aplicación más popular de esta ley es la deformación de resortes sin embargo la ley de Hooke se puede utilizar en:
- Ingeniería de materiales
- Arquitectura
- Construcción
- Industria automotriz
- Elaboración de dinamómetros
- Sismología
- Mecánica molecular
- Acústica
No solo en estas áreas se hace el estudio, también ha servido para la creación de elementos como:
- Balanza de resorte
- Manómetro
- Galvanómetro
- Volante del reloj mecánico
Sin dudas los aportes que realizó Robert Hooke hace más de 400 años siguen aplicándose hoy en día con más y más elementos.
Ley de Hooke en los resortes
Sin duda alguna la forma más conocida de representar matemáticamente esta ley, aquí se relaciona la fuerza ejercida por el resorte con la elongación o alargamiento provocado por la fuerza externa aplicada al extremo:
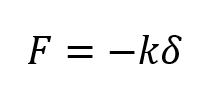
Donde k es la constante elástica del resorte cuyas unidades son N/m normalmente y δ es la elongación o el cambio de longitud que experimenta con unidades en metros.
El signo negativo en la ecuación significa que, en relación con la posición de reposo, la dirección de deflexión de un resorte es opuesta a la fuerza del mismo. En otras palabras si se amarra un objeto a un resorte y se intenta mover hacía abajo la fuerza que hará el resorte será hacía arriba, así mismo se mueve el objeto hacía la derecha el resorte hará la fuerza hacía la izquierda.
Antes de continuar debemos explicarte algo relacionado con los resortes.
¿Qué es un resorte?
También conocidos como muelles en algunos lugares del planeta, los resortes son objetos que pueden ser deformados por una fuerza externa y volver a su forma original en ausencia de dicha fuerza.
Hay muchísimas clases de resortes sin embargo el más conocido y con el que más se trabaja como estándar internacional es el resorte en espiral de metal, estos se utilizan desde fabricación de relojes hasta fabricación de colchones.
La elasticidad que tiene el resorte no se debe a la geometría que tiene sino que es una propiedad del metal, el hecho de enrollar lo que facilita es tener una gran cantidad de materia en un pequeño espacio.
Física de la deformación del resorte
Cuando se le aplica una fuerza externa al resorte este empieza a deformarse, se conoce como deformación elástica cuando el resorte recupera la forma inicial, deformación elástico-plástica cuando se realiza un esfuerzo intermedio que no produce una deformación irreversible pero tampoco una recuperación total de la forma inicial.
La deformación plástica se produce cuando se aplica una fuerza tan alta que el resorte no recupera su forma inicial, de hecho después de esto se considera que el resorte deja de funcionar, finalmente si la fuerza es muy alta se llega a la tensión de rotura donde el resorte rompe.
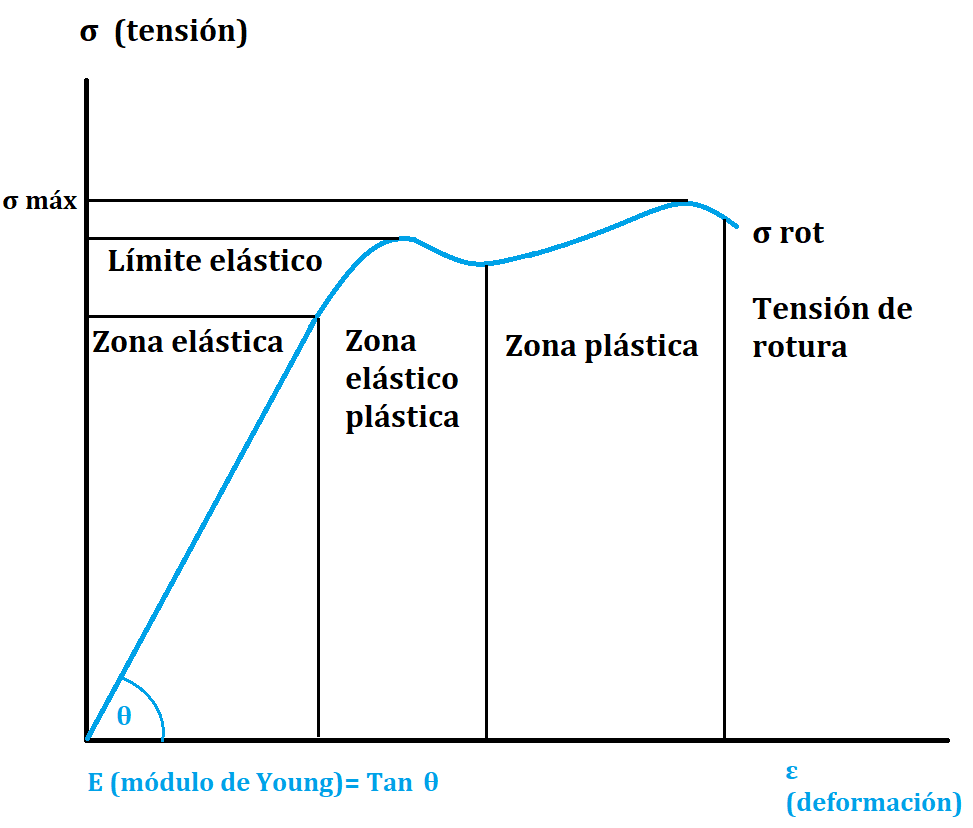
Este comportamiento es de suprema importancia ya que la Ley de Hooke solo se cumple en la zona elástica, cuando el resorte llega a la zona elástico-plástica, a la zona plástica o a la zona de ruptura la ley deja de cumplirse.
Variables de estudio
Cuando se hace el estudio a un resorte se hace en términos de esfuerzo o tensión, representado con la letra griega sigma σ y la deformación o alargamiento representado con la letra griega épsilon, ε.
Esfuerzo
Es la fuerza que se le aplica a una superficie de la sección transversal del resorte, por ejemplo si un resorte está elaborado de alambre si se aplica una fuerza F el esfuerzo será mayor si el área transversal del alambre es de 1 mm2 que si es de 5 mm2.
Una misma fuerza generará menor esfuerzo entre más grueso sea el alambre del cual está hecho un resorte.
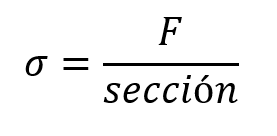
Deformación
Es la relación entre la variación de longitud y la longitud total del alambre del cual está hecho el resorte, por ejemplo un resorte que se alarga 5 cm y tiene una extensión total de 1 metro sufre mayor deformación que otro resorte que se alarga los mismos 5 cm pero que tiene una extensión de 5 metros.
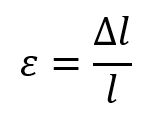
Módulo de Young
A partir de la relación entre la tensión y la deformación se obtiene el modulo de Young que se escribe con el símbolo E:
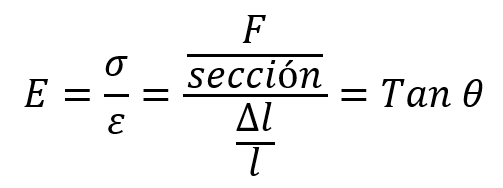
El módulo de elasticidad o módulo de Young permite conocer la resistencia de un material a ser deformado.
Este módulo fue desarrollado por Thomas Young en el siglo XVII, es constante si se cumple la ley de Hooke, de ser así existe una relación entre la constante del resorte, el área, la longitud y el módulo de Young, esta relación se puede expresar como:
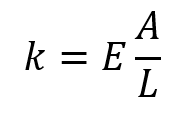
Energía potencial elástica de un resorte
Cuando un resorte es comprimido acumula energía que se libera cuando este recupera nuevamente su forma original, la ecuación que representa la energía potencial elástica del resorte es:
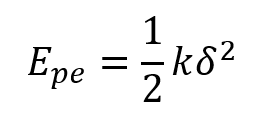
Esto se puede utilizar para conocer la energía con la que un cuerpo sale despedido cuando un resorte aplica no una fuerza en contra del movimiento natural sino a favor del mismo.
Resortes en serie
En ocasiones se requiere poner dos o más resortes en serie, es decir el final de uno conecta con el inicio de otro, por ejemplo
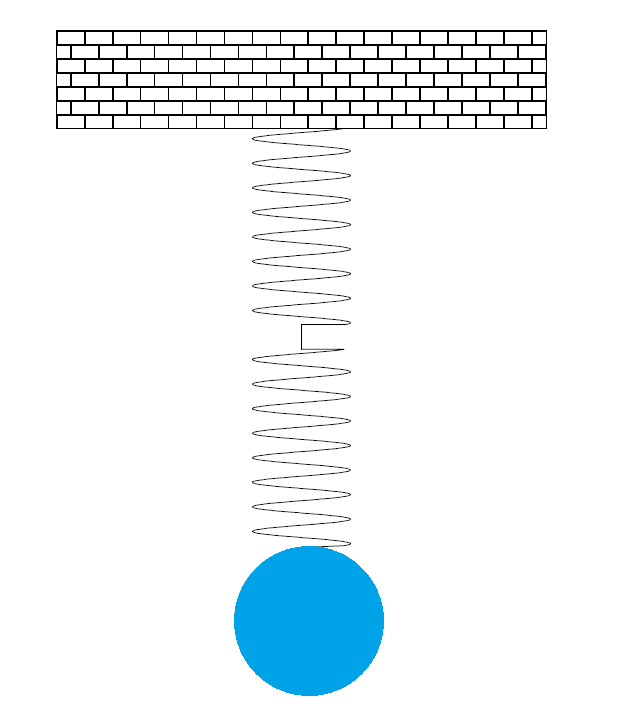
En estos casos la constante k global va a ser equivalente a la constante k del resorte dividido entre el número total de resortes:
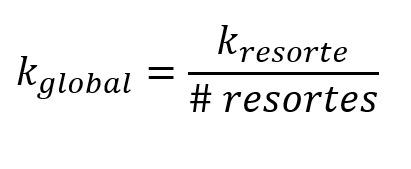
Resortes en paralelo
Cuando se ubican los resortes en paralelo, es decir que comparten el mismo inicio y el mismo final la constante k global también cambia:
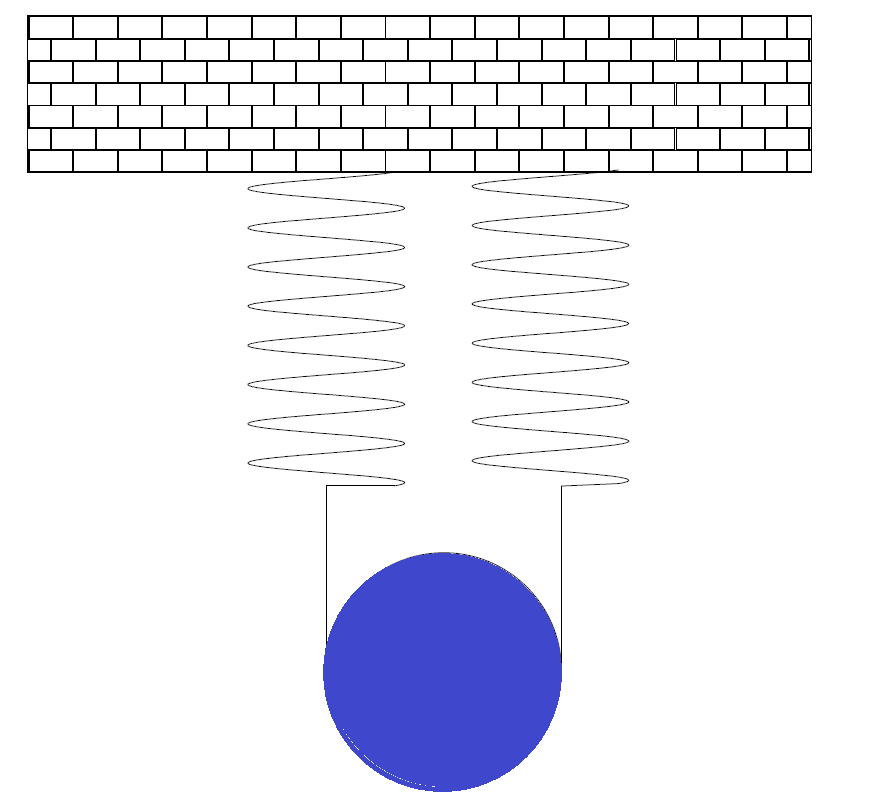
En estos casos la constante k global va a ser equivalente a la constante k del resorte multiplicado por el número total de resortes:

Ejercicios resueltos
Cálculo de la constante k
¿Cuál es la constante k de un resorte que mide 50 cm en reposo, que cuando se le cuelga un cuerpo de 1 kg la longitud es de 100 cm?
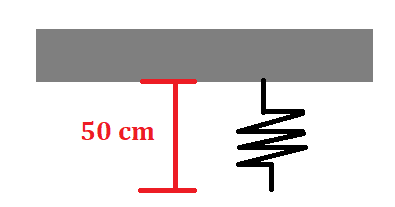
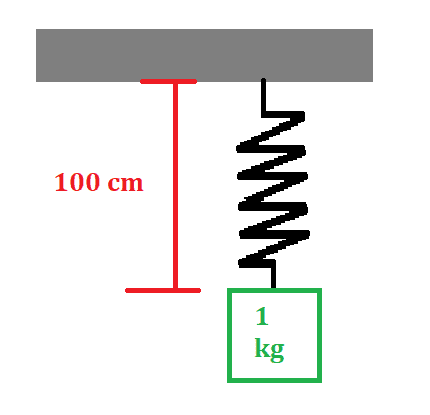
Solución
Se plantea la ley de Hooke para resortes
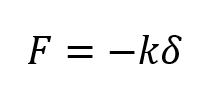
La fuerza que ejerce el peso es la masa (1 kg) multiplicado por la gravedad (-9,81 m/s2)
En este caso la gravedad hace que el cuerpo vaya hacía abajo, el signo es negativo ya que está en un sentido opuesto a la fuerza que hace el resorte (hacía arriba) luego:
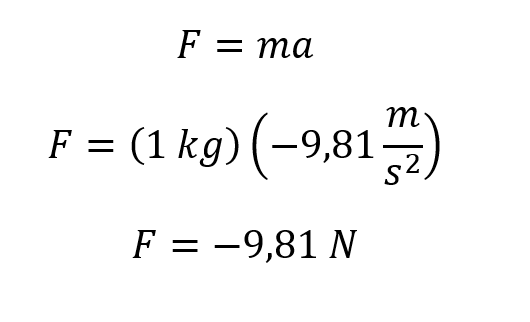
Recuerda que la masa en kg multiplicada por la aceleración en m/s2 da como resultado kg-m/s2 que equivalen a Newton, la fuerza se mide en Newton, si tienes dudas sobre el tema de unidades te invitamos que leas nuestro artículo sobre magnitudes fundamentales y derivadas.
Volvemos a la ley de Hooke:
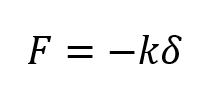
Conocemos ahora el valor de la fuerza y el delta, es decir la diferencia de longitudes del resorte con peso y sin peso así que reemplazamos los valores:
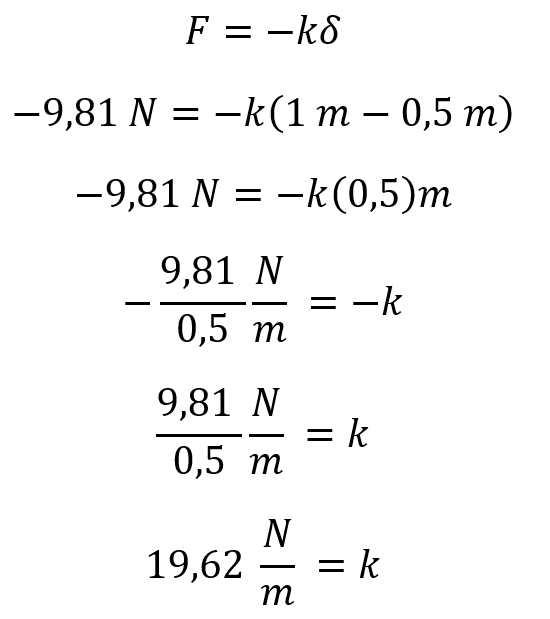
Los cálculos se deben realizar en metros por eso 100 cm = 1 m y 50 cm = 0,5m de este modo podemos conocer que la constante k= 19,62 N/m
Pregunta b:
¿Cuál será la longitud del mismo resorte si ahora se cuelga un cuerpo de 5 kg?
Solución
Nuevamente para este caso se plantea inicialmente la ley de Hooke
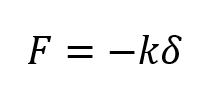
Se calcula la fuerza que ejerce el cuerpo de 5 kg
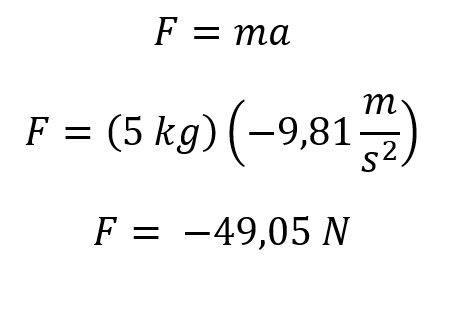
Como es el mismo resorte conocemos que la constante k es igual a 19,62 N/m por lo que la ecuación de Hooke queda:
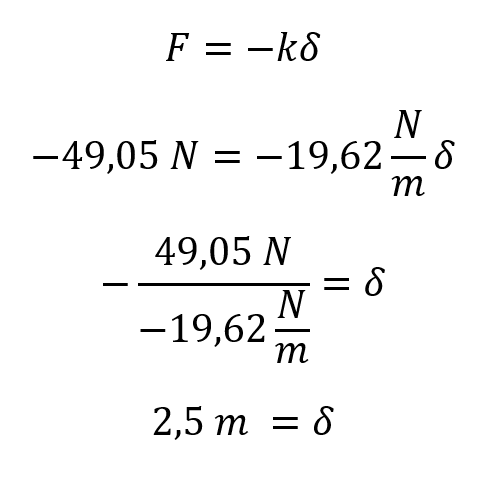
El delta de elongación es igual a 2,5 metros pero esa no es la longitud final del resorte, recordemos que:

Con una masa de 5 kg la longitud final del resorte será de 3 metros.
Cálculo de energía potencial elástica
Un resorte con constante k= 500 N/m que se encuentra ubicado horizontalmente y fijo en uno de sus extremos, se comprime 8 centímetros.
Si se pone una cuerpo esférico de 200 gramos y se libera el resorte ¿a qué velocidad saldrá disparado el cuerpo?
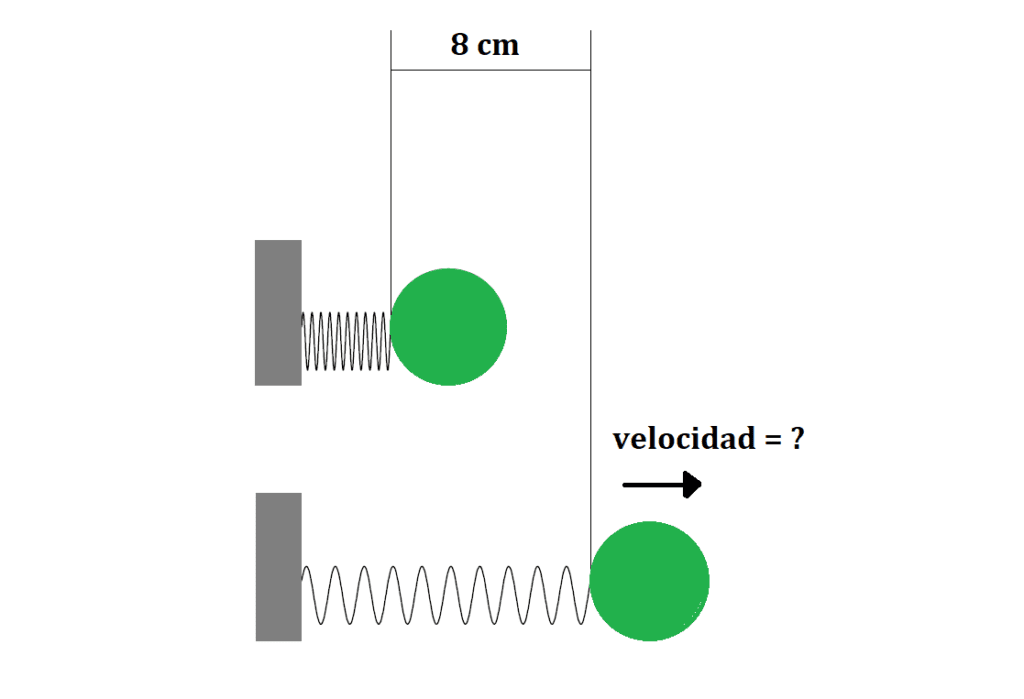
Solución
Lo primero que se calcula es la energía potencial elástica del resorte
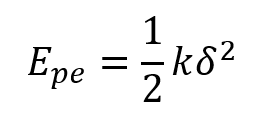
Recordemos que los centímetros se deben pasar a metros por lo que 8 cm es igual a 0,08 metros
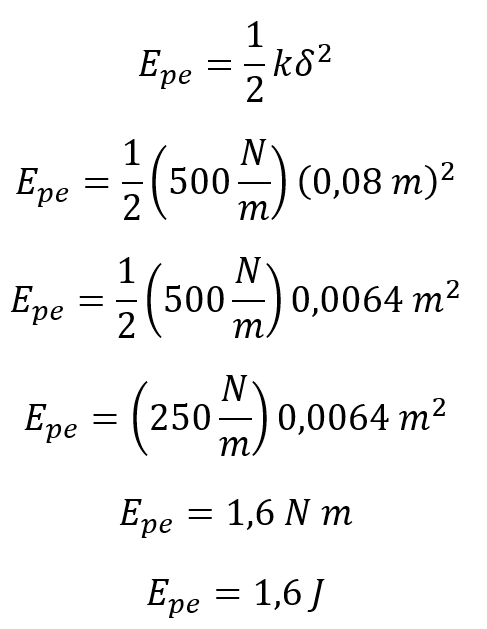
La fuerza en Newton multiplicada por metros da como resultado kg-m2/s2 que equivalen a Joules, la energía se mide en Joules.
Si tienes dudas sobre el tema de unidades te invitamos que leas nuestro artículo sobre magnitudes fundamentales y derivadas.
La energía potencial elástica del resorte se convierte en energía cinética para el cuerpo esférico:

Por lo que podemos despejar la velocidad del cuerpo ya que conocemos la masa (0,2 kg) las unidades de masa son los kilogramos puedes aprender aquí del Sistema Internacional de Unidades

El cuerpo esférico saldrá disparado con una velocidad de 4 m/s.
Cálculo con resortes en serie y en paralelo
Se tienen tres resortes, cada uno de 10 centímetros y con una constante k de 1200 N/m.
Si son configurados en serie para colgar un cuerpo de 10 kg ¿Cuál será la distancia a la que queda el cuerpo? ¿Cuál será si se ubican los resortes en paralelo?
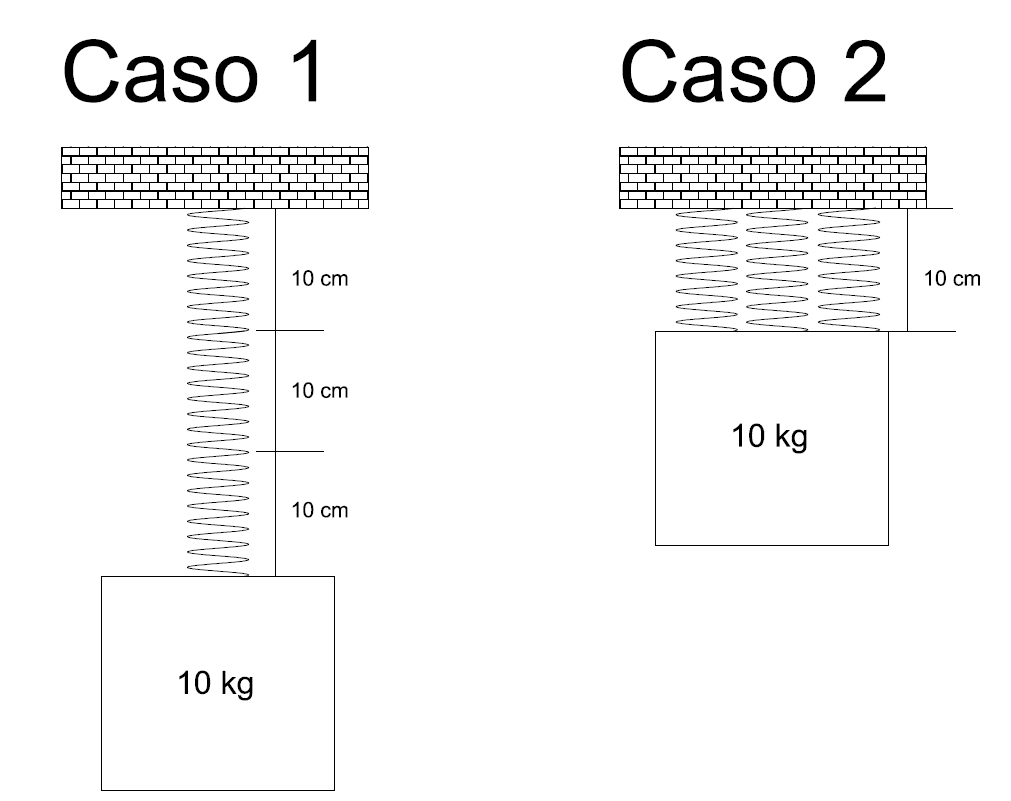
La gráfica muestra el estado inicial, una vez se cuelgan las masas de 10 kg se empieza a elongar el resorte.
Vamos a calcular inicialmente la configuración en serie.
Resortes en serie
El primer paso es calcular la fuerza que ejerce la masa de 10 kg
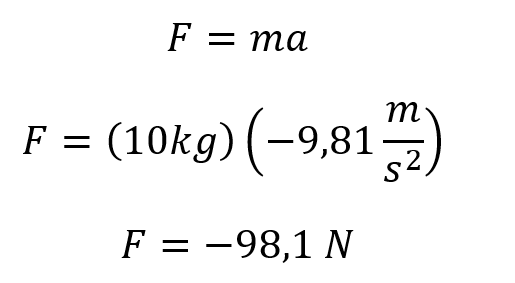
Luego se calcula el k global
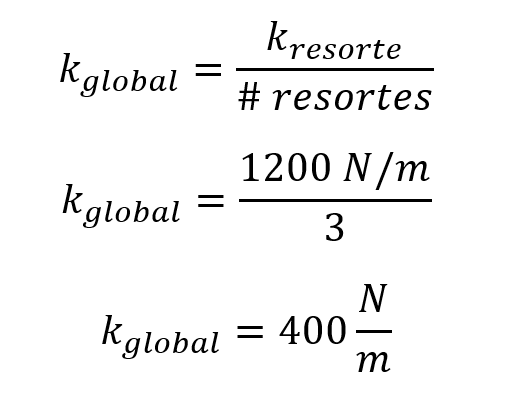
Se aplica la ley de Hooke
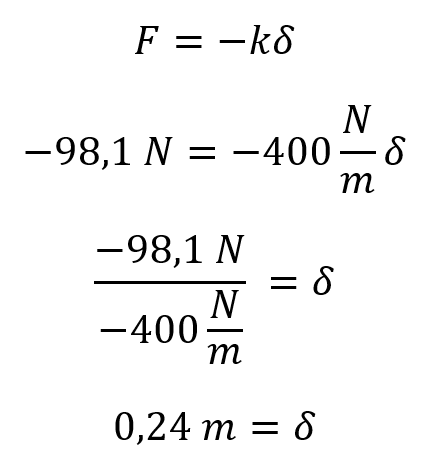
La longitud final de los resortes será:

Resortes en paralelo
La masa es la misma que en serie por lo que la fuerza que ejerce el cuerpo va a ser también -98,1 N.
Se calcula entonces la constante k para resortes en paralelo
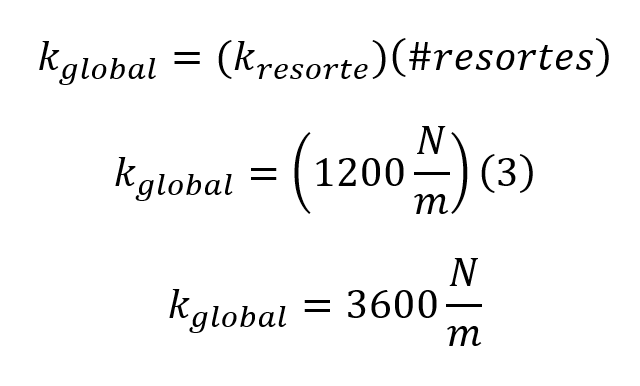
Se aplica la ley de Hooke
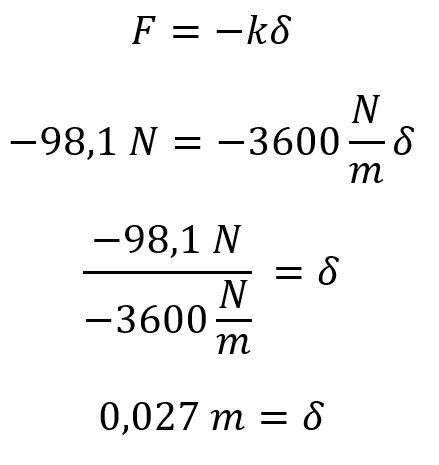
La longitud final de los resortes será:

¿Cómo referenciarnos?
Si deseas incluir esta información en alguno de tus trabajos no olvides referenciarnos, puedes hacerlo así:
Munévar, R. (7 de abril de 2024) Ley de Hooke. Ecuacionde.com. Recuperado el día/mes/año (inserta aquí la fecha del día que consultas nuestra web) de https://ecuacionde.com/hooke
Gracias por visitar nuestra página web.
Te invitamos a seguir descubriendo nuestro contenido

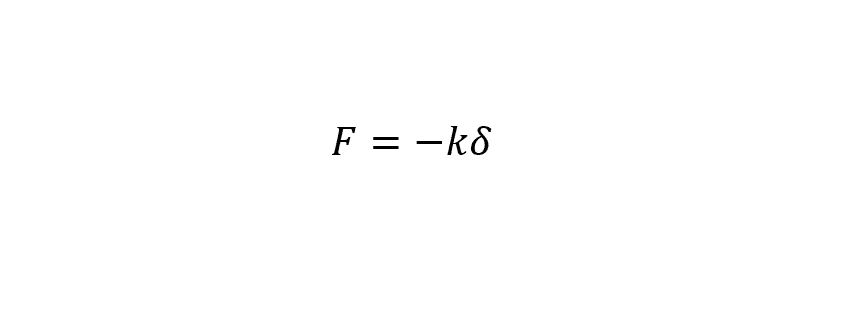

Muy ilustrativo el tema. Gracias. Nos ayudan a superarnos en estos temas de muchísimo interés.