El grado de incertidumbre de una medida está implícito en la forma en la que esta se expresa, cuando se toma una medida solo se pueden dar con certeza cierta cantidad de dígitos, después, cuando se hacen cálculos matemáticos con esa medida la cantidad de dígitos y el error puede propagarse, de allí que es importante conocer realmente cuáles son las cifras significativas.
Tabla de contenidos
¿Qué son las cifras significativas?
Son los dígitos de una medida que aportan alguna información, debido a esto también se puede decir que son el conjunto de dígitos que se conocen con seguridad en una medida.
De acuerdo con el Sistema Internacional de Unidades, todas las medidas deben ser expresadas en su número correcto de cifras significativas
¿Cómo se determinan?
Existen tres reglas para generales para determinar la cantidad de cifras significativas que tiene un número, estas son:
- Los dígitos diferentes de cero siempre son significativas
- Los ceros entre dos cifras significativas también son significativos
- Los ceros al final de la parte decimal son significativos
Adicional a las reglas que existen es muy importante utilizar la lógica cuando se trate de determinar la cantidad de valores significativos, por ejemplo si se utiliza una regla común y corriente no se puede obtener como resultado una medida de 16,3051548996532109 centímetros porque la regla no tiene forma de presentar toda esa cantidad de decimales.
Desde el punto de vista técnico y científico solo se presentan dígitos que tienen un sentido lógico de acuerdo con el instrumento utilizado en la medición.
Regla 1: los dígitos diferentes de cero siempre son significativos
Esta tal vez es una regla que parece lógica sin embargo muchas personas no la tienen en consideración, por ejemplo si se hace una medición con cualquier instrumento (regla, balanza, termómetro, etc.) y este arroja un número en el resultado diferente de cero automáticamente cada dígito se convierte en una cifra significativa, por ejemplo:
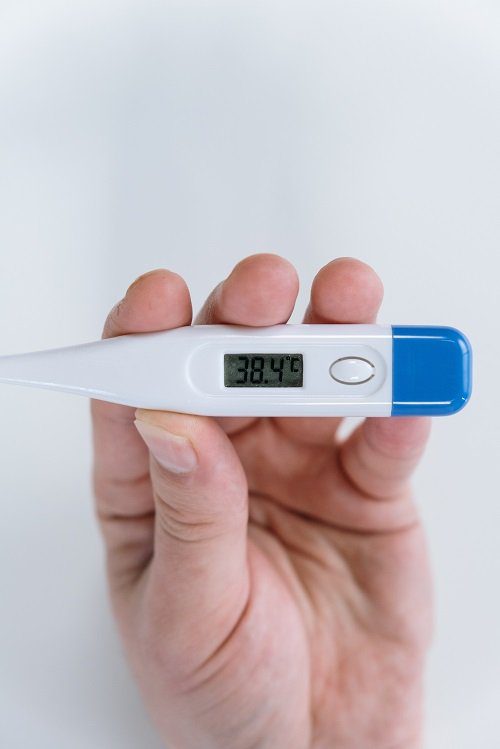
El termómetro está marcando 38,4°C, todos los dígitos son diferentes de cero por lo que esa medición tiene tres valores significativos.
Por ejemplo si el termómetro marcara 39,43°C entonces esa medición tendría cuatro valores significativos, si marcara 124,58°C entonces tendría cinco y así sucesivamente.
La dificultad radica por ejemplo cuando se hacen otro tipo de mediciones, supongamos en una balanza

En este caso la balanza marca 6,9201 gramos ya aparece el dígito cero por lo que debemos ver otras reglas para determinar la cantidad de cifras significativas.
Regla 2: cualquier cero entre dos cifras significativas también son significativos
Teniendo en cuenta la medición anterior realizada en la balanza, como resultado se obtuvo una masa de 6.9201 gramos, en este caso significa que hay 6 unidades, 9 decimos, 2 centésimos, 0 milésimos y 1 diezmilésimo de gramos.
La regla 1 nos decía que cualquier dígito diferente de cero era una cifra significativa, en la medida de la balanza tenemos los dígitos:
6: Significativo de acuerdo con la regla 1
9: Significativo de acuerdo con la regla 1
2: Significativo de acuerdo con la regla 1
0: ¿Es o no es significativo? ya lo veremos
1: Significativo de acuerdo con la regla 1
La regla 2 nos dice que cualquier cero entre dos cifras significativas también son significativos, en este caso el cero está entre el número 2 y el número 1, ambos significativos por lo tanto en este caso el cero también es una cifra significativa.
En conclusión el número 6,9201 tiene 5 cifras significativas.
Algunos otros ejemplos donde el cero es significativo:
Cuando se hace una medición de un objeto con una regla y se tiene como resultado:

En este caso la medición de la regla es de 10,5 centímetros nuevamente se hace el análisis de la regla 2:
1: Significativo de acuerdo con la regla 1
0: Significativo de acuerdo con la regla 2 ya que está en medio de dos cifras significativas.
5: Significativo de acuerdo con la regla 1
La regla 2 nos dice que cualquier cero entre dos cifras significativas también son significativos, en este caso el cero está entre el número 1 y el número 5, ambos significativos por lo tanto en este caso el cero también es una cifra significativa.
En conclusión el número 10,5 tiene 3 cifras significativas.
A este tipo de ceros en alguna literatura se les conoce como «ceros apresados».
¿Ahora qué pasa si los ceros no se encuentran entre dos números significativos? por ejemplo si hacemos una medición con una balanza analítica y se obtiene una masa de 0,0321 gramos ¿Cuántos números son significativas?

0: No se encuentra entre dos significativos, no es significativo
0: No se encuentra entre dos significativos, no es significativo
3: Significativo de acuerdo con la regla 1
2: Significativo de acuerdo con la regla 1
1: Significativo de acuerdo con la regla 1
En conclusión, el número 0.0321 tiene tres cifras significativas.
Regla 3: los ceros al final de la parte decimal son significativos
Cuando se hace una medición y el instrumento con el cual se toma la medida arroja ceros en la parte decimal son considerados cifras significativas, a diferencia de los que están antes de la parte decimal por ejemplo se toma una medida con un micrómetro dando como resultado 0,00300 entonces:
- 0: No se encuentra entre dos significativos, no es significativo (regla 2)
- 0: No se encuentra entre dos significativos, no es significativo (regla 2)
- 0: No se encuentra entre dos significativos, no es significativo (regla 2)
- 3: Significativo de acuerdo con la regla 1
- 0: Significativo de acuerdo con la regla 3
- 0: Significativo de acuerdo con la regla 3
De este modo la medición con un micrómetro cuando marca 0,00300 tiene tres cifras significativas (se resaltan en negrita los ceros que sí son significativos)
Supongamos que se hace una medición con un micrómetro y se obtiene la cifra a continuación:

En este caso la medición que se está haciendo es exactamente 25.000 todos los números tienen un significado por lo que tendría 5 cifras significativas que se describirían así:
- 2: Significativo de acuerdo con la regla 1
- 5: Significativo de acuerdo con la regla 1
- 0: Significativo de acuerdo con la regla 3
- 0: Significativo de acuerdo con la regla 3
- 0: Significativo de acuerdo con la regla 3
Si se escribiera en notación científica se deberían mantener los ceros de la precisión en la medida es decir el número es 2,5000 x 102
Casos especiales en las reglas
En ocasiones hay números especiales que se deben tener en cuenta para determinar las cifras significativas, especialmente en los ceros.
Ceros cuando el número es menor que uno:
Por ejemplo cuando un número es muy pequeño (menor que uno) normalmente tiene varios ceros, por ejemplo:
0,00745
0,000024450
0,000039874
En estos casos esos ceros no son significativos, solo están para denotar espacios vacíos más no involucran decisiones en las mediciones.
Cero de la unidad
Cuando un número empieza por cero esa cifra puntualmente no es significativa, por ejemplo:
023,45
0,458
01
En estos casos esos ceros tampoco son cifras significativas.
Ceros que no son de una medición
Existen cantidades que no fueron tomadas a partir de una medición sino que simplemente se da el número, cuando sucede eso los ceros a la derecha no son cifras significativas, por ejemplo:
En una conversación entre dos amigos:
Persona A: ¿Cuántos metros crees que hay en esa calle?
Persona B: No sé, deben haber unos 200
No se realizó una medida para tomar la cifra 200 por lo tanto:
2: Significativo de acuerdo con la regla 1
- 0: No se encuentra entre dos significativos, no es significativo (regla 2)
- 0: No se encuentra entre dos significativos, no es significativo (regla 2)
- Por lo que en ese caso solo tendría una cifra significativa, si se hubiera tomado la distancia con la ayuda de un metro el 200 tendría 3 cifras significativas.
Cifras significativas en números exactos
Cuando se tiene un número exacto por definición se asume que ese valor tiene infinitas cifras significativas ya que no son mediciones sino valores que son absoluta verdad sin necesidad de medición, por ejemplo:
- En esa habitación hay 20 personas
- En un milenio hay 1000 años
- Esa resma de papel tiene 500 hojas
En estos casos 20, 1000 y 500 tienen infinitas cifras significativas. Otros ejemplos en donde sucede lo mismo es en las conversiones de unidades como por ejemplo:
- 1 pie son 12 pulgadas
- 1 metro son 100 centímetros
- 1 hora son 60 minutos
En estos casos 12, 100 y 60 tienen también infinitas cifras significativas.
¿Por qué son importantes las cifras significativas?
La cantidad de cifras significativas depende de la precisión del instrumento de medición, esto es de vital importancia ya que un error en la medición podría llevar incluso hasta la muerte.
Por ejemplo a un bebé se le recetan 0,05 gramos de una medicina llamada difenhidramina para aliviarle la tos que tiene hace 3 días, sin embargo la única balanza que se tiene para medir el medicamento es la siguiente:

La persona encargada de administrar el medicamento procede con el peso hasta que la balanza marca 1 gramo, sin embargo como sabe que 0,05 gramos es menor retira un poco de medicamento y procede a administrárselo al bebé.
El resultado es el fallecimiento del bebé por intoxicación de difenhidramina, en la autopsia se determina que ingirió 0,75 gramos, 15 veces la dosis que le fue recetada porque no se tuvieron en cuenta los valores significativos.
Reglas para el redondeo
En ocasiones se presentan casos cuando al realizar operaciones matemáticas con números se presentan en los resultados cifras con más de seis dígitos, debido a esto es importante saber redondear para acortar el número a una cantidad de cifras más manejable.
Por ejemplo si se tiene 6,48498464565654124537 muchas de las cifras puede que no sean representativas para el cálculo, si se dijera que se va a trabajar con 4 cifras significativas quedaría reducido a 6,485 que es un número más manejable.
Cuando se redondea se está cambiando el valor exacto del número por lo que es importante hacerlo de tal forma que afecte el resultado lo menor posible, para hacerlo correctamente se deben realizarlos siguientes pasos, vamos a tomar como ejemplo la cantidad redondeada 6,48498464565654124537 a cuatro cifras significativas donde quedó 6,485
- Se establece cuántas cifras significativas se quieren dejar
- Se evalúa el dígito a la derecha de la cantidad de cifras que se van a dejar
- Si el dígito es menor que 5 (es decir 0, 1, 2, 3 o 4) se elimina ese dígito y todos los demás de ahí hasta el final hacía la derecha.
- Si el dígito es mayor que 5 (es decir 6, 7, 8, o 9) se aumenta en 1 el digito anterior y se eliminan todos los siguientes
- Si el dígito es igual a 5, el dígito anterior se deja igual si es par o se le suma 1 si es impar y se eliminan todos de ahí a la derecha.
Vamos a ver algunos ejemplos para que quede más claro cada uno de los casos.
Ejemplo 1:
Redondear a 3 cifras significativas el número 4,1231893123:
Lo primero que se debe hacer es ver cuál dígito coincide con la cantidad de cifras significativas que nos piden para el caso el tercer dígito:
4,1231893123 en el dos marcado con negrita estarían las 3 cifras significativas
Las reglas nos dicen que revisemos el dígito de la derecha, es decir el cuarto dígito
4,1231893123 el cuarto dígito es un 3, como es menor que 5 entonces se elimina ese dígito y todos los demás de ahí hasta el final hacía la derecha
4,12 sería el valor redondeado a 3 cifras significativas.
Ejemplo 2:
Redondear a 5 cifras significativas el número 1,10359128:
Lo primero que se debe hacer es ver cuál dígito coincide con la cantidad de cifras significativas que nos piden para el caso el quinto dígito:
1,10359128 en el cinco marcado con negrita estarían las 5 cifras significativas
Las reglas nos dicen que revisemos el dígito de la derecha, es decir el sexto dígito
1,10359128 el sexto dígito es un nueve, como es mayor que 5 entonces se aumenta en 1 el digito anterior y se eliminan todos los siguientes
1,1036 sería el valor redondeado a 5 cifras significativas
Caso especial: en este punto te podrás preguntar ¿Qué pasa si el número anterior es 9? vamos a mostrar cómo se redondea, supongamos entonces que nos piden redondear 1,10399128 a cinco cifras significativas.
Lo primero que se debe hacer es ver cuál dígito coincide con la cantidad de cifras significativas que nos piden para el caso el quinto dígito:
1,10399128 en el cinco marcado con negrita estarían las 5 cifras significativas
Las reglas y nos dice que revisemos el dígito de la derecha, es decir el sexto dígito
1,10399128 el sexto dígito es un nueve, como es mayor que 5 entonces se aumenta en 1 el digito anterior y se eliminan todos los siguientes, pero el dígito anterior es un 9 ¿Qué hacer ahí? tranquilo, no hay problema funciona igual que la suma, el 9 al que se le suma 1 pasa a cero y aumenta el número de atrás, es decir el 3 pasa a ser 4.
1,1040 sería el valor redondeado a 5 cifras significativas, recuerda que según la regla 3 el último cero es una cifra significativa.
Ejemplo 3
Redondear a 4 cifras significativas el número 2,3615
Lo primero que se debe hacer es ver cuál dígito coincide con la cantidad de cifras significativas que nos piden, para el caso el cuarto dígito:
2,3615 en el uno marcado con negrita estarían las 4 cifras significativas
Las reglas nos dicen que revisemos el dígito de la derecha, es decir el quinto dígito
2,3615 el quinto dígito es un cinco, como es exactamente 5 se debe evaluar si el número anterior es par o impar, el cuarto número es 1, que es impar por lo que se le suma una unidad y se elimina el resto de valores.
2,362 sería el valor redondeado a cuatro cifras significativas
Operaciones matemáticas con números significativos
Cuando se tienen números o mediciones con cierto grado de precisión pueden tener diferente cantidad de cifras significativas por lo que es importante conocer cómo hacer las operaciones matemáticas con estos resultados.
Suma y resta
Para la suma y la resta de acuerdo con las cifras significativas solo se tienen en cuenta la cantidad de dígitos después de la coma, por ejemplo si se quieren sumar:
11,38
4,4
Se hace un análisis de la cantidad de dígitos después de la coma, el primer número tiene dos dígitos después de la coma, el segundo dígito tiene un solo dígito después de la coma.
Se soluciona como una suma tradicional:
11,38+4,4=15,78
Se redondea el resultado con la cantidad menor de dígitos después de la coma, en ese caso se debe dejar solo un dígito.
11,38+4,4= 15,8
Ejemplo 2:
Se quiere restar 9,4589 y 6,111 entonces lo primero es analizar la cantidad de dígitos después de la coma
9,4589 tiene 4 dígitos después de la coma
6,111 tiene 3 dígitos después de la coma
Se hace la resta normal 9,4589 – 6,111 = 3,3479
Se redondea a la menor cantidad de dígitos que para este caso es 3 después de la coma, entonces:
9,4589 – 6,111 = 3,348
Ejemplo 3:
Se quiere restar 14 y 3,95 entonces lo primero es analizar la cantidad de dígitos después de la coma
14 no tiene ningún dígito después de la coma
3,95 tiene dos dígitos después de la coma
Se hace la resta normal 14 – 3,95 = 10,05
Se redondea a la menor cantidad de dígitos que para este caso es cero después de la coma, entonces:
14 – 3,95 = 10
Multiplicación y división
En la multiplicación y división se determinan las cifras significativas de cada uno de los números involucrados en la operación, el resultado debe tener la misma cantidad de números significativos del número original que menos tenga.
Ejemplo 1:
Se quiere multiplicar 4,433 x 5,1 entonces lo primero es determinar la cantidad cifras significativas
4,433 tiene cuatro cifras significativas
5,1 tiene dos cifras significativas
Se realiza la multiplicación normal 4,433 x 5,1 = 22,6083
Se redondea hasta la menor cantidad de cifras significativas en este caso dos, quedando
4,433 x 5,1 = 23
Ejemplo 2:
Se quiere dividir 62,43 entre 3,01 entonces lo primero es determinar la cantidad de números significativos
62,43 tiene cuatro cifras significativas
3,01 tiene tres cifras significativas
Se realiza la división normal 62,43 / 3,01 = 20,7408637873….
Se redondea hasta la menor cantidad de cifras significativas en este caso tres, quedando
62,43 / 3,01 = 20,7
¿Cómo referenciarnos?
Si deseas incluir esta información en alguno de tus trabajos no olvides referenciarnos, puedes hacerlo así:
Munévar, R. (7 de abril de 2024) Cifras Significativas. Ecuacionde.com. Recuperado el día/mes/año (inserta aquí la fecha del día que consultas nuestra web) de https://ecuacionde.com/cifras-significativas
Gracias por visitar nuestra página web.
Te invitamos a seguir descubriendo nuestro contenido